From Zero to One

首先我必须声明的一点是：往后的所有文章、记录均非博客、知识讲述系列；仅仅用于我个人的学习记录和体会。因此其中的一些知识并非全面且准确的。

本学习笔记的起名DDCA是有着一定含义的：其一，是ETHz(苏黎世联邦理工学院)的一门课Digital Design and Computer Architecture； 同时也是一本入门书籍Digital Design and Computer Architecture的名字。对于笔者而言，这也是我的第一门系统性的Architecture课程和阅读书籍。

笔者真心的希望，该阅读笔记能够对你有所帮助。同时，本笔记采用中英结合的方式，尽量的不会对读者对于原著的理解有过多偏差。

The GAME PLAN

本节讲述了全书的目标：如何设计和构建自己的微处理器(how to design and build your own microprocessor)。该书致力于描述数字系统的设计，尤其是如何在1，0的机器上运行。

并且，本节也指出了数字系统的一个很大的优点就是足够简单，只有1和0。当然，这和后面的数字系统中的二进制系统有很大关系，也涉及到了布尔代数(这一点我们后面再谈)。

The Art of Managing Complexity

One of the characteristics that separates an engineer or computer scientist from a layperson is a systematic approach to managing complexity.

将工程师或计算机科学家从外行人中分离出来的特征之一是管理复杂性的系统方法。也就是说，你需要学习去了解如何构建微处理器，而不会陷入其中细节的泥潭。

显而易见的，这些概念在生活、学习和项目中是十分常见的。我们需要确定一个明确的目标，同时也需要一个良好的层次抽象(Hierarchical Abstraction)。

Abstraction

The critical technique for managing complexity is abstraction: hiding details when they are not important.

管理复杂性的关键技术在于抽象(Abstraction): 在不重要的时候隐藏细节(或者说，隐藏一些不重要的细节)。一个系统通常能从许多不同的抽象层次来看待：

  • 比如电子计算机系统的抽象层次，以及每个层次的经典构建(由上到下)：
    • Application Software, Programs
    • Operator Systems, Device Drivers
    • Architecture, Instructions Registers
    • Micro-architecture, Datapaths Controllers
    • Logic, Adders Memories
    • Digital Circuits, AND Gates and NOT Gates
    • Analog Circuits, Amplifiers Filters
    • Devices, Transistors Diodes
    • Physics, Electrons

最底层的抽象是物理学，也就是电子的运动。电子的行为是由量子力学和麦克斯韦方程组描述(Quantum mechanics and Maxwell’s equations)。我们的系统是由晶体管(或真空管(已经淘汰))等电子器件(electronic devices)构建的。

再下一个抽象层是模拟电路(Analog Circuits)，各种器件被组装以创建放大器等组件，模拟电路输入和输出一个连续的电压范围。

而数字电路(Digital circuits) 将电压限制在离散范围内，我们将用它来表示0和1。在后续的逻辑层(Logic)中，我们会从数字电路中构建更复杂的结构，如加法器或存储器。

微架构(Micro-architecture)将抽象的逻辑层和架构层联系起来。架构层(Architecture)的抽象是从程序员的角度来描述一台计算的。微架构涉及组合逻辑元素(combining logic elements)来执行架构定义的指令。

对于软件层和操作系统层，这里就不再赘述。本书主要集中关注数字电路通过计算机体系结构的抽象层次(focuses on the levels of abstraction from digital circuits through computer architecture.)。

在具体介绍更为详细的内容前，有一句话值得深思：

When you are working at one level of abstraction, it is good to know something about the levels of abstraction immediately above and below where you are working.

Discipline

Discipline is the act of intentionally restricting your design choices so that you can work more productively at a higher level of abstraction.

规训(Discipline，其实笔者更愿意叫做规约)有意限制你的设计选择的行为，这样你就可以在更高的抽象层面上更有效地工作。

这句话是较为难理解的，这句话强调了在设计和实现过程中要考虑到上层需求和可替代性，以便在提供抽象接口给上层时，能够让上层用户更加灵活、高效地使用。规约的设计和实现可以确保在更高的抽象层面上工作时不会出现不必要的复杂性和混乱。

结合上述，在本书的内容中，数字上的规约是十分重要的：我们考虑到数字电路上使用离散电压，而模拟电路使用连续电压。因此，数字电路是离散电路的一个子集。从某种意义上说，数字电路必须具备比更广泛的模拟电路类别更少的能力。

那么，我们就应该选择模拟电路作为规约了吗？不对，然而数字电路更更更容易去设计，对于数字电路，我们可以容易地将元件组合成复杂的系统，最终在许多应用中优于由模拟电路构建的系统。因此，回归主题，本书是以数字电路为载体研究计算机结构的。

The Three-Y’s

除了抽象和规约，设计者们还会使用三个y's来管理复杂性：层次性(Hierarchy)、模块性(Modularity)和规律性(Regularity)：

  • 层次性是指将一个系统划分成为模块，然后队每个模块进行进一步细分，直到各部分易于理解。
  • 模块化是指模块具有定义良好的功能和接口，因此它们很容易地连接在一起，而不会产生意想不到的副作用。
  • 规律性是指寻求模块之间的统一性。公共模块被多次复用，减少了必须设计的不同模块的数量。

我猜，肯定有人会不理解层次性居然是划分模块，而不是分层级。实际上，这里的模块指的就是一般意义上的层级，比如说add，sub就可以看作两个模块，而这两个模块同属于function模块。如上所述，这样就分为了两个层级。

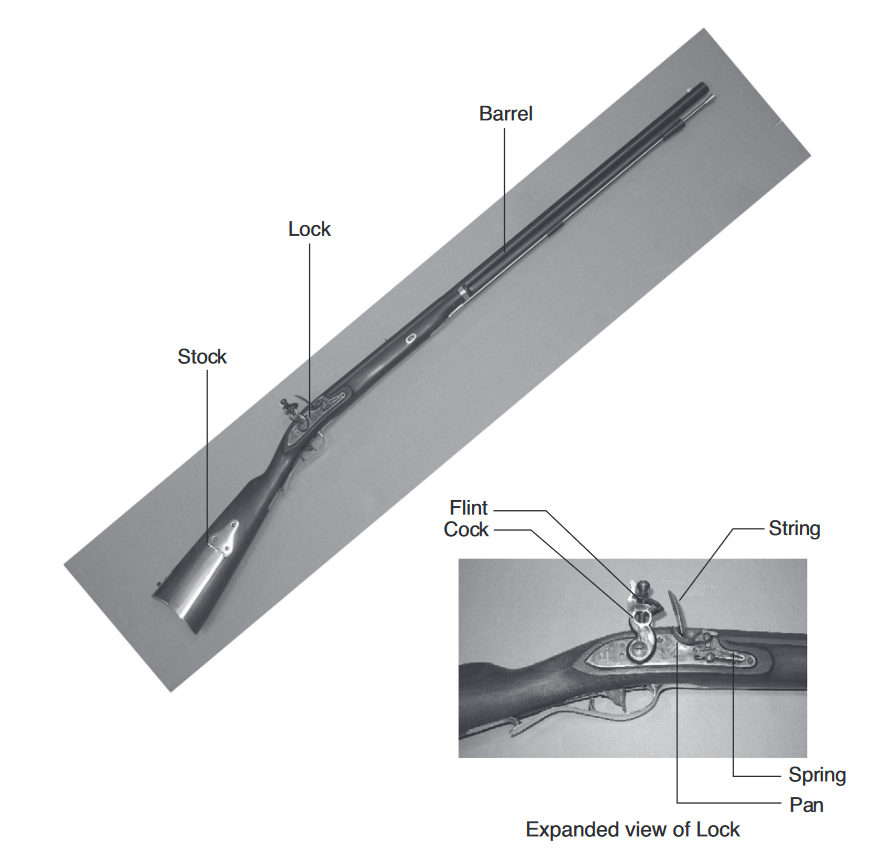
Flintlock rifle with a close-up view of the lock

上图是原书中的例子，这里做一个简要介绍：

  • 以层次性来说
    • 来复枪分为三个组件：Stock、Lock、Barrel
      • Barrel为发射子弹的金属长管
      • Lock可以分为：Flint、Cock、String、Sprint和Pan
      • Stock将零件固定在一起，提供安全抓力的木制本体
    • 每个组件都可以被进一步详细地分层描述
  • 以模块化来说
    • 每个组件都应该具有明确定义的功能和接口
      • Stock的功能是组装Lock和Barrel，其接口由长度和安装引脚位置组成
      • Barrel的功能是给子弹施加旋转，使其更加精确地运动
      • …
    • 模块化要求不应该有副作用：Stock的设计不应该方案Barrel的功能
  • 以规律性来说
    • 一个损坏的Barrel可以由一个相同的部分来代替，Stock可以在装配线上高效地建造，而不是费力地手工

The Digital Abstraction

Most physical variables are continuous. For example, the voltage on a wire, the frequency of an oscillation, or the position of a mass are all continuous quantities. Digital systems, on the other hand, represent information with discrete-valued variables—that is, variables with a finite number of distinct values.

对于数字系统(digital system)，其用离散值变量表示信息的——即具有有限个不同值的变量。

而不同于Babbage's machine，大多数电子计算机采用二进制(two-valued)表示，其中高电压表示1，低电压表示0。

Babbage's machine

假设信息量为$D$(the amount of information D)，那么$N$个不同状态的离散值变量中的信息量$D$以比特(bit)为单位进行度量:

$$
D = \log_2N \ bits
$$

所以，一个二进制变量传递的信息量为$\log_22 = 1 \ bit$(事实上，bit这一单位就是由binary digit的缩写)。

一个连续的信号理论上包含无穷的信息量，因为它可以取无穷多个值(A continuous signal theoretically contains an infinite amount of information because it can take on an infinite number of values.)。 但在实际应用中，对于大多数连续信号，噪声和测量误差将信息限制在$10 \thicksim 16 \ bits$。如果你想要快速传递信息，那么该信息量需要更低(比如说$8 \ bits$)。

本书关注的是使用二进制变量：1和0的数字电路，而Boole开发了一种对二进制变量进行操作的逻辑系统，被称为布尔逻辑(Boolean Logic)。

每一个布尔变量都是TRUE或者FALSE。电子计算机通常使用正电压表示1，零电压表示0。因此，在本书以及本笔记中，我们会同义地使用术语1、TRUE和HIGH；当然0、FALSE和LOW也是如此。

程序员可以在不需要了解计算机硬件的详细细节的情况下进行工作。另一方面，了解硬件的细节可以让程序员更好地针对特定计算机进行软件优化。

Number Systems

对于大多数人工作在十进制系统的情况不同，我们通常会工作在十六进制或者二进制下。所以，不会有人还要被教吧？

Decimal Numbers

我们以$K$表示系数，$10$表示基数，$n$代表权重，那么就可以得出十进制的表示方法：

$$
K_n10^n \cdot K_{n-1}10^{n-1} \cdot … \cdot K_210^2 \cdot K_110^1 \cdot K_010^0 \cdot K_{-1}10^{-1} \cdot K_{-2}10^{-2} \cdot … \cdot K_{-n+1}10^{-n+1} \cdot K_{-n}10^{-n}
$$

Binary Numbers

和十进制一样，不过我们需要把基数换为$2$：

$$
K_n2^n \cdot K_{n-1}2^{n-1} \cdot … \cdot K_22^2 \cdot K_12^1 \cdot K_02^0 \cdot K_{-1}2^{-1} \cdot K_{-2}2^{-2} \cdot … \cdot K_{-n+1}2^{-n+1} \cdot K_{-n}2^{-n}
$$

Hexadecimal Numbers

不多赘述：

$$
K_n16^n \cdot K_{n-1}16^{n-1} \cdot … \cdot K_216^2 \cdot K_116^1 \cdot K_016^0 \cdot K_{-1}16^{-1} \cdot K_{-2}16^{-2} \cdot … \cdot K_{-n+1}16^{-n+1} \cdot K_{-n}16^{-n}
$$

Bytes, Nibbles, and All That Jazz

虽然我们了解了数字系统，不过我们也应该了解一些在计算机数字系统中的一些术语。

一个$8 \ bits$的组被称为$1 \ byte$。其表示范围为：$2^8 = 256$。存储在计算机内存中的对象大小通常以byte而不是bit来衡量。

一个$4 \ bits$的组，或者说半字节(half a byte)被称为$1 \ nibble$(这应该算是老古董的衡量单位了，现在已经不在使用)。

微处理器以被称为字(words)的块来处理数据，一个word的大小取决于微处理器的体系结构。

微处理器是建立在单芯片上的处理器。直到1970’s为止，处理器过于复杂，不再适合单芯片上运行。
在本笔记中，我们将交替使用微处理器和处理器两个术语。

在一组bits中，1(这里指的是位数，而非是从右到左第一个为1的)所在列的比特位被称为最小有效位数(the least significant bit, lsb)，而另一端的比特位被称为最大有效位(the most significant bit, msb)；类似地，在一个word中，也有最低有效字节(the least significant byte, LSB)和最高有效字节(the most significant byte, MSB)。

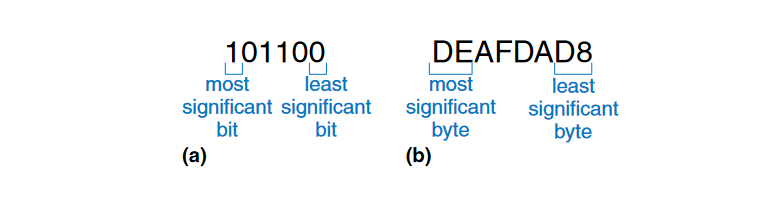
Least and most significant bits and bytes

巧合的是，$2^{10} = 1024 \approx 10^3$。因此，术语kilo表明$2^{10}$。与此类似的是：MB、Mb、GB和Gb分别表示$2^{20}bytes$、$2^{20}bits$、$2^{30}bytes$和$2^{30}bits$。

Binary Addition

这一块没什么说的，就是正常的计算。

Signed Binary Numbers

我们有两种方法表示有符号二进制数：Sign/Maganitude和Two's complement。

Sign/Magnitude Numbers

一个$N-bit$的sign/magnitude数使用最高符号位作为符号位，剩余的$N-1 \ bits$作为幅度(也就是绝对值)。

值得注意的是：正常的二进制加法在sign/magnitude数中不起作用，同时具有正零和负零之分。

Two’s Complement Numbers

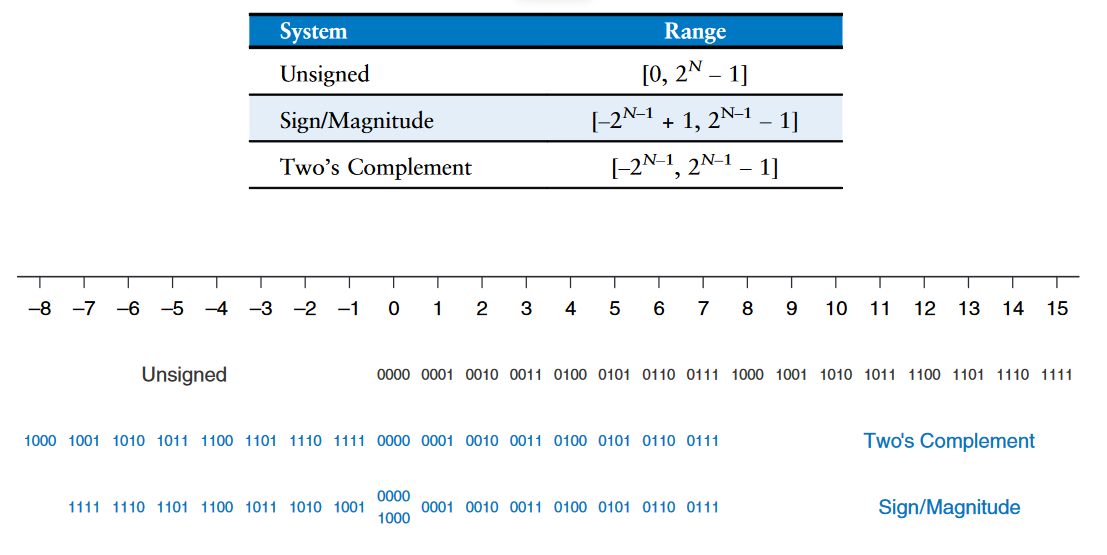
二进制补码(Two's complement)数克服了sign/magnitude数的问题，其表示的容量范围为：$[2^{N-1}, 2^{N-1} - 1]$。

  • 二进制补码的表示方法分为两类：
    • 如果该二进制数是正数(包括0)，那么不变
    • 如果该二进制数是负数
      • 使用1作为充当符号位的数
      • 其余位正常表示后，除符号位取反加一即可

对于补码来说，还可以用于检测加减法是否溢出(overflow)：

  • 溢出的判别方法：
    • 溢出只存在于同符号的加减中。
    • 如果两个数的符号位相同，计算后结果的符号位不同，则发生溢出。

同时，补码还有另外一个特点：符号扩展(signed extension)，当一个补码数扩展到更多位时，必须将符号位从当前位置依次复制到msb上。

Comparison of Number Systems

Comparison Numbers

Logic Gates

Now that we know how to use binary variables to represent information, we explore digital systems that perform operations on these binary variables.

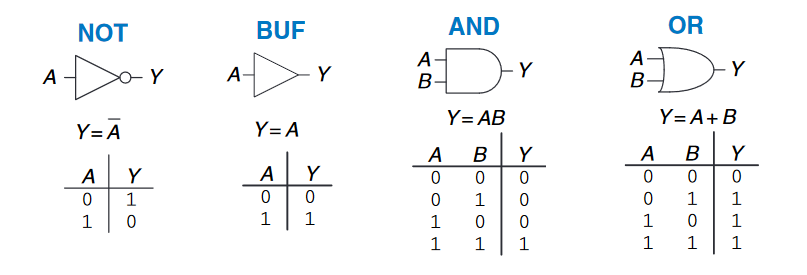
逻辑门(Logic Gates)是取一个或多个二进制输入并产生一个二进制输出的简单数字电路。逻辑门是用符号表示输入和输出的。

Gates

NOT Gate

非门(NOT Gate)有一个输入$A$和一个输出$Y$。关于非门的描述不做过多介绍，非门也被称为逆变器(inverter)。本笔记中，我们使用$Y = \overline{A}$作为非门的记号。

Buffer

缓冲器(buffer)只是简单的将输入复制到输出。有的人可能会问，“这个有存在的必吗？”。当然的，存在就必有其价值：从模拟的角度上看，缓冲器可能具有理想的特性，例如能将大量的电流传递给电机等。如果单单只是从逻辑上看，缓冲器与导线并没有什么区别。这就是为什么我们需要从多层次的了解系统的一个例子：数字抽象掩盖了缓冲器的实际目的。

AND Gate

与门(AND Gate)有两个输入和一个输出。我们通常使用$Y = AB$来表示。

OR Gate

或门(OR Gate)和与门一致，我们使用$Y = A + B$来表示。

Other Two Input Gates

至于下面的二输入逻辑门，不再过多赘述，请自行查阅。

Other Gates

Beneath The Digital Abstraction

一个数字系统使用离散值变量，然而，变量使用连续的物理量来表示的。这就导致一些问题：在真实的系统中存在许多噪声，如果假定$5V = 1$，那么$4.97V$也应该表示$A = 1$？$4.3V$呢？或者更一点的值呢？

Supply Voltage

假设系统中的最低电压为$0V$，其称为groud或GND；系统中的最高电压来自于电源，通常被称为$V_{DD}$。目前，电源电压的值随着时代的发展在逐步降低。

Logic Levels

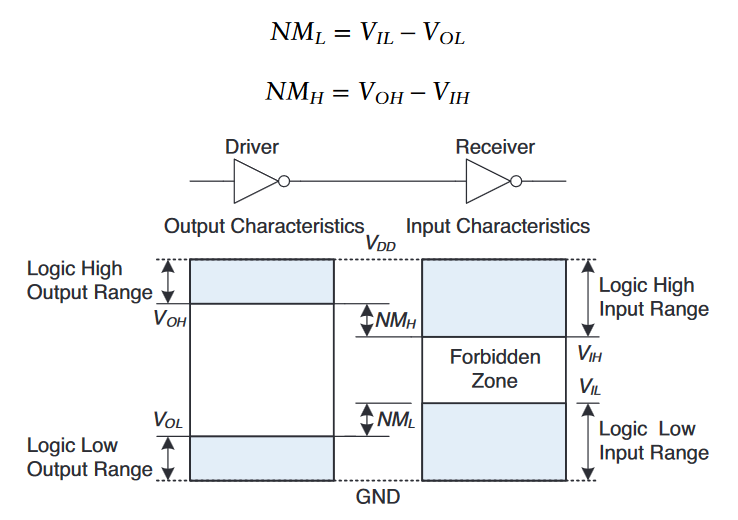
连续变量到离散变量的二元映射是通过定义逻辑层次(Logic Levels)来完成的。如下图所示，第一个门被称为driver，而第二个门被称为receiver。

假设driver的输出范围为$0 \thicksim V_{OL}$的电压就可以表示输出了LOW(0)，输出范围为$V_{OH} \thicksim V_{DD}$的电压表示输出了HIGH(1);而receiver接收到范围为$0 \thicksim V_{IL}$的电压表示输入LOW(0)，接收到范围为$V_{IH} \thicksim V_{DD}$的电压表示输入HIGH(1)。

由于噪声或者故障原件等原因，接收器的输入应该落在范围为$V_{IL} \thicksim V_{IH}$的禁区(forbid)内，表示门的行为此时是不可预测的。现在我们称$V_{OL}$、$V_{OH}$、$V_{IL}$和$V_{IH}$分别为输出和输出的高、低逻辑电平。

Logic levels and noise margins

Noise Margins

为了保障即使环境内存在故障或噪声，但是其影响不那么大时，逻辑门的功能仍然能够正常运行。我们应该有一个被称为噪声容量(noise margin)的概念：在最坏的情况下的输出中可以添加的噪声量。

如上图所示，当我们的输入在$V_{OL} \lt NM_{L}$和$V_{OH} \gt NM_{H}$时，接收器的输入仍然能够检测到正确的逻辑电平。

$V_{DD}$表示金属氧化物半导体晶体管漏极(drain)上的电压，用于构建大多数现代芯片，有时也被称为$V_{CC}$；
$GND$表示金属氧化物半导体晶体管源极(source)上的电压，有时也被称为$V_{SS}$。

DC Transfer Characteristics

为了理解数字抽象的限度，就必须深入研究门的模拟行为。栅极(gate)的直流转移特性(direct current transfer characteristics)将输出电压描述为输入电压的函数，当输入足够慢时，其输出可以保持不点。这一点描述了输入输出的特性，因此被称为特性转移。

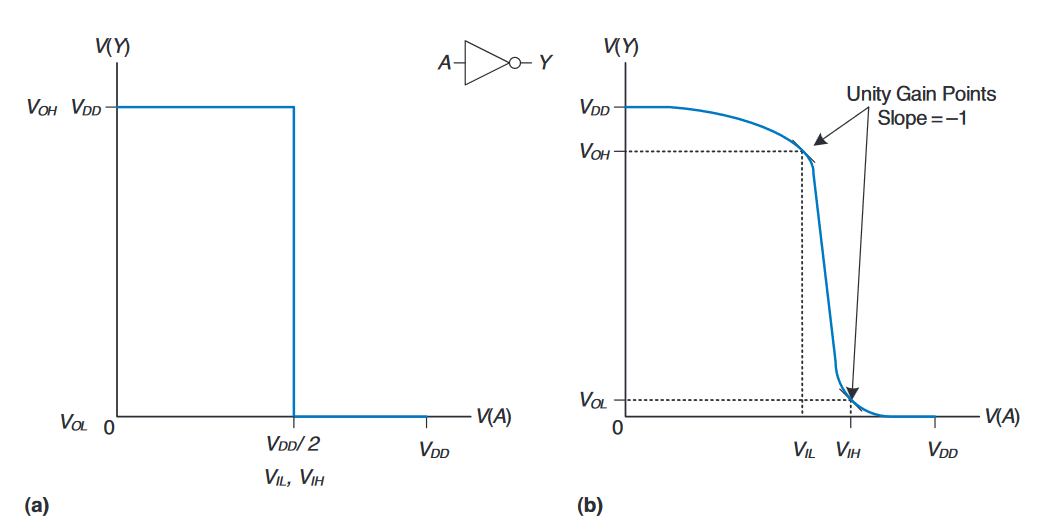
DC transfer characteristics and logic levels

也就是上图所示，在理想情况当$V(A) \lt V_{DD} / 2$时，$V(Y) = V_{DD}$。此时，$V_{IH} = V_{IL} = V_{DD} / 2$，$V_{OH} = V_{DD}$以及$V_{OL} = 0$。

但实际上，由于各种原因，这些端点之间的转换是平滑的(也就是说，并非会直接以图a折线的方式转换)，可能并不完全以$V_{DD} / 2$为中心。

选择逻辑电平的合理位置是传输特性$dV(Y)/dV(A)$的斜率为$-1$时，这两个点被称为单位增益点(unity gain points)。在单位增益点处选择逻辑电平通常会使噪声容量最大化。

The Static Discipline

为了避免输入落入禁区，数字逻辑门在设计之初就有着一个准则：给定逻辑上有效的输入，那么每一个电路元件都会产生逻辑上有效的输出。

数字设计者通过遵循静态规训，牺牲了使用任意模拟电路元件的自由，以换取数字电路的简单性和鲁棒性。(By conforming to the static discipline, digital designers sacrifice the freedom of using arbitrary analog circuit elements in return for the simplicity and robustness of digital circuits.)

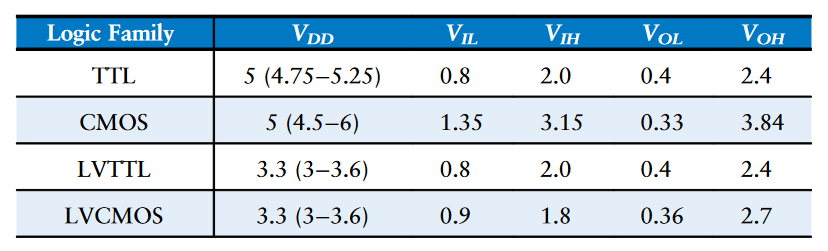
$V_{DD}$和逻辑电平的选择使任意的，但所有的通信门都必须具备兼容的逻辑电平。因此，门被划分到逻辑家族(logic families)中：

Logic levels of 5 V and 3.3 V logic families

CMOS Transistors

现代计算机使用晶体管，因为它们便宜、小巧而且可靠。晶体管是在控制端施加电压或电流时，使开关导通或关闭的电控开关。

常见的有两种主要类型的晶体管：双极晶体管(bipolar junction transistors)和金属氧化物半导体效应晶体管(metal-oxide-semiconductor field effect transistors)，后者一般被叫做MOSFETs或MOS transistors。

本节，我们将在数字抽象的下方窥探逻辑门是如何从MOS中构建出来的。

Semiconductors

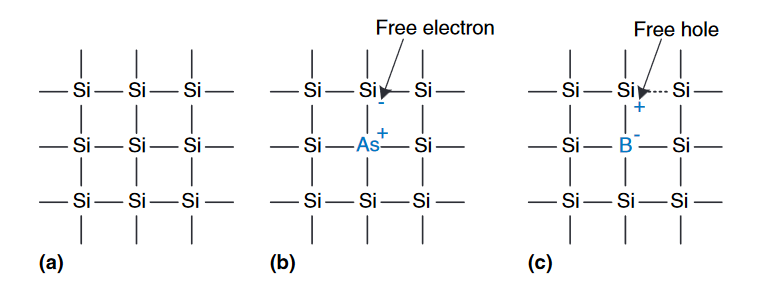
MOS晶体管是由原子硅构成的，硅($Si$)是Ⅳ族原子，因此其价电子层有四个电子，并与相邻的四个原子形成键，从而形成晶格。

就其本身而言，硅是一种不良导体，因为所有的电子都是以共价键结合在一起的。当仔细地添加少量的杂质，即掺杂原子时，它就会成为一个更好的导体。

如果加入Ⅴ族掺杂剂(比如$As$)，掺杂剂原子有一个不参与成键的额外电子(free electron)。电子可以很容易的绕过晶格移动，留下一个电离的掺杂原子($As^{+}$)，如下图b所示。由于这个自由电子携带的是负电(Negative charge)，因此我们称为n-type掺杂剂，而构建的半导体被称为n-type半导体。

另一方面，如果加入Ⅲ族掺杂剂(比如$B$)，掺杂剂原子缺少一个电子，这个缺失的电子被称为空穴(hole)。一个来自邻近硅原子的电子可以移动过来填充缺失的键，形成一个离子化的掺杂原子($B^{-}$)，并在该邻近硅原子处留下一个空穴。空穴可以在晶格周围移动，并且，空穴是缺乏负电荷的，因此其就像一个带正电荷的粒子。因此，我们将该掺杂剂称为p-type掺杂剂，而构建的半导体称为p-type半导体。

由于硅的电导率随着掺杂剂的浓度变化而在多个数量级上变化，因此硅被称为半导体。

Silicon lattice and dopant atoms

Diodes

现在我们已经知道：$n-type$半导体中有游离的电子，而$p-type$半导体中有游离的空穴。

当我们将$n-type$和$p-type$连接时，由于材料中载流子(空穴和电子)的浓度不同，会发生载流子的扩散。具体来说，$p-type$中的空穴会向$n-type$扩散，而$n-type$中的电子会向$p-type$扩散。这种扩散导致了在PN结(PN junction)附近形成了一个带电荷的区域。

在$PN$结形成的过程中，当$p-type$中的空穴与$n-type$中的电子重新结合时，会产生正负电荷相互抵消的情况，形成一个无载流子的区域，这被称为耗尽区。在耗尽区内部，形成了一个内建电场，内建电场阻止了进一步的载流子扩散，因此PN结具有一定的单向导电性质。

因此，只有当外加电压且$P$区加正电、$N$区加负电(外加电压大于内建电场电压)时，自由电子才会远远不断的流向$P$区，就产生了从$P \longrightarrow N$的电流。如果反向加电压，那么会给内建电压助力，如果反向电压过高，那么内场就会被击穿。因此，二极管具有单向导电性。下图中的二极管图片很形象的描述了这一性质。

diodes

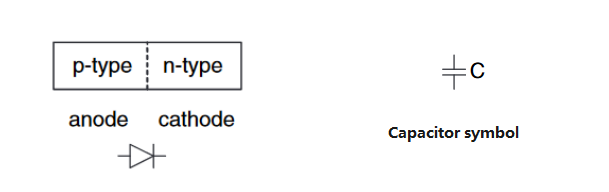
p-n junction and capacitor

Capacitors

电容器由绝缘体隔开的两个导体组成。当对其中一个导体施加电压$V$时，该导体积聚电荷$Q$，另一个导体积聚相反的电荷$-Q$。电容器的电容$C$为电荷与电压的比值：

$$
C = \frac{Q}{V}
$$

电容的符号如上图所示。电容很重要，因为对导体充电或放电需要时间和能量。更多的电容意味着电路将更慢，需要更多的能量来运行。

nMOS and pMOS Transistors

我们先来了解一下$n-type$的制作过程和原理。

如下图所示，$nMOS$的绝大部分以p-type作为底物(substrate)，在底物的两侧有两个n-type，在底物的上方覆盖一层二氧化硅绝缘体，再在其上方填充一层多晶硅(Polysilicon)。我们使用金属导体分别在两个n-type和多晶硅上引出金属电极。

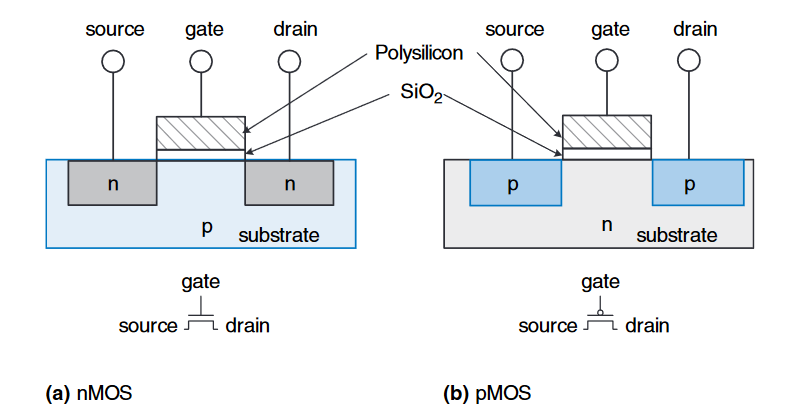
nMOS and pMOS transistors

其中一个被称为源极(source)，另一个称为漏极(drain)；由多晶硅引出的金属导体被称为栅极(gate)。底物通常接地也就是GND。

我们发现，$nMOS$的两个n-type和底物p-type刚好形成两个方向相反二极管。这就导致了，当栅极接地时，其中一个二极管是导通的，另外一个二极管就是截止的。因此，源极和漏极不导通，无电源流通；当栅极连接电源时，由于栅极现在积攒正电荷，而中间有一层绝缘体，因此在下方的$p-type$底物上就会吸引负电荷累积将空穴赶走，当自由电子累积的足够多时，就形成了如下图b展示的通道(channel)，这里是$n-channel$。现在就有了一条从$n-type$源极开始途径$n-channel$到$n-type$漏极的连续的通道，电流就可以从源极流向漏极，此时该$nMOS$就是导通的，也就是$ON$的。

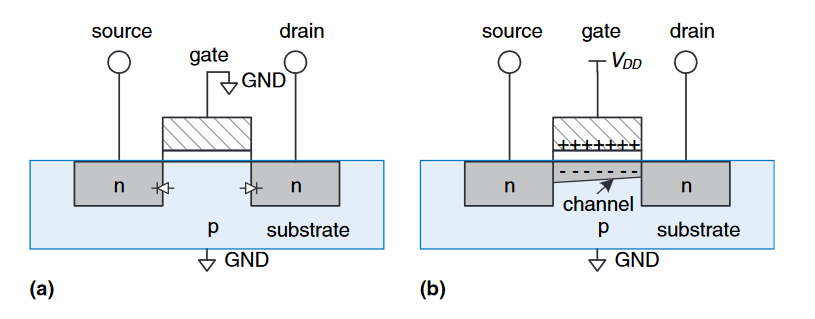
nMOS transistor operation

而$pMOS$的制作和原理仅仅是$n-type$换为$p-type$即可，当栅极接地时，源极和漏极导通；当栅极连接电源时，源极和漏极截止。

因此，$MOS$晶体管的表现为电压控制开关，其中栅极电压产生电场，使源极和漏极之间的连接导通或关断。效场应晶体管(field effect transistor)就来源于这一工作原理。

晶体管开启所需的栅极电压称为阈值电压(threshold voltage, $V_t$)，通常为$0.3 \thicksim 0.7V$。

不幸地是，MOSFETs并非是完美的开关(switches)。以下是其的一些主要原因：

  • 导通状态的抗阻问题：
    • 在开关应用中，理想情况下希望开关关闭时有很高的阻抗以防止电流流动，而开关打开时有很低的阻抗以便电流通过。MOSFETs在导通时有相对较低的导通阻抗，但它们在关闭时的阻抗可能相对较高，这可能会导致一些能量损失
  • 静态功耗
    • 即使MOSFET处于关闭状态，仍然存在漏电流，这可能导致一些静态功耗。虽然这种功耗相对较小，但在某些应用中可能是一个问题，尤其是对于需要长时间保持关闭状态的应用
  • 体效应
    • MOSFET的导通状态是通过施加栅极电压来控制的，这可能受到称为“体效应”的影响。当栅极电压较低时，由于电荷积累在栅极和沟道之间的绝缘层中，MOSFET的阻抗可能会增加，这可能会导致开关性能不稳定
  • 电压和电流的关系
    • 在某些情况下，MOSFET的导通特性可能不完全符合理想的线性关系。这可能导致在特定电压下，电流并不严格地按照预期的方式变化，这可能会导致一些设计上的挑战

为了在同一芯片上同时构建两种类型的晶体管，制造过程通常以一个$pMOS$开始，然后在$pMOS$会途径的地区植入被称为well(实际上我不知道该怎么翻译)的$nMOS$。这种同时提供两种不同类型的晶体管的这些工艺被称为互补金属氧化物半导体(Complementary MOS)或CMOS。$CMOS$工艺被用于构建当今制造的所有晶体管中的绝大多数。

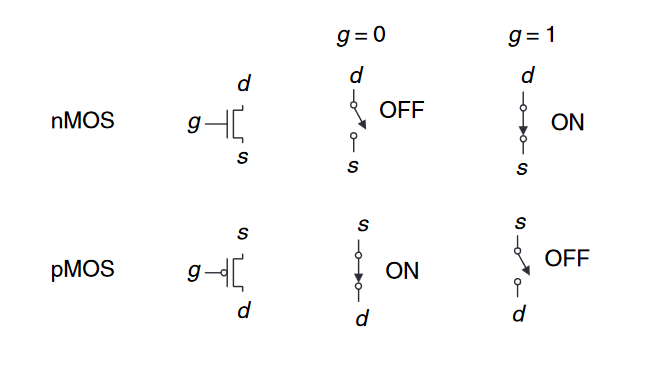
Switch moduels of MOSFETs

CMOS NOT Gate

由下图中的左图可以看出，如果$A = 0$，$N1$是断开的而$P1$是导通的，因此$Y$就会和$V_{DD}$导通呈现上拉(pulled-up)逻辑1；相反的，$A = 0$，$Y$就会与$GND$导通呈现下拉(pulled-down)逻辑0。

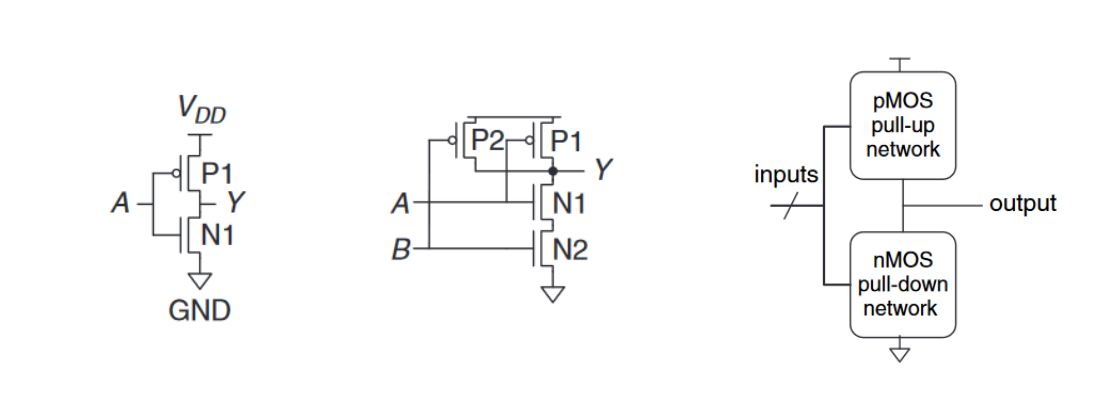
CMOS Gates

Other CMOS Logic Gates

上图中的中间一图展示了二输入的$NAND$门，但是我在这里就不再过多赘述。

最右图展示了用于构建任意反转逻辑门的一般形式(如$NOT$, $NAND$或$NOR$)。

$nMOS$晶体管善于传递0(这里是如何理解呢，是因为当输入为$A=1$时，$nMOS$中的$n-channel$形成，内部是传递0的)，因此在输出$Y$和$GND$之间放置了一组$nMOS$晶体管的下拉网格，以将输出拉低为0。$pMOS$晶体管善于传递1，因此在输入$V_{DD}$和输出$Y$之间放置了一组$pMOS$晶体管的上拉网格，以将输出上拉为1。网格可以由串联或并联的晶体管组成。

如果上拉网格和下拉网格同时导通，$V_{DD}$和$GND$之间将发生短路(short circuit)。当然，栅极的输出可能处于禁区，那么晶体管造成大量功耗，可能足以烧毁。

另一方面，如果上拉网格和下拉网格同时断开，则输出既不连接$V_{DD}$也不连接$GND$。这时我们就说输出是浮动(floating)的，其值是未定义的。浮动输出通常是不被希望的，但是在后面我们也会介绍一些关于浮动输出的特例(偶尔也可以作为优势，就比如你的bugs一样)。

在一个正常工作的逻辑门中，对于任意给定的时刻，如果其中一个网络是$ON$的，那么另一个网络就应该是$OFF$的，这样输出就可以被拉高或拉低，而不是短路或浮动的。我们可以通过导通互补规则(the rule of conduction complements)来保证这一点：当$nMOS$晶体管串联时，$pMOS$晶体管必须并联；当$pMOS$晶体管并联时，$pMOS$晶体管必须串联。

Transmission Gates

有时，设计者发现使用一个能够良好传递0和1的理想开关很方便。回顾一下，$nMOS$晶体管擅长传递0，而$pMOS$晶体管擅长传递1， 因此两者的并联组合可以很好地传递这两个值。下图中的左图显示了这样一个电路，称为传输们(Transimission Gate)或通门(pass gate)。 开关的两侧称为$A$和$B$，因为开关是双向的，没有首选输入或输出侧。控制信号称为使能(enables)，$EN$和$\overline{EN}$。当$EN = 0$且$\overline {EN} = 1$时，两个晶体管都关闭。因此，传输门处于关闭或禁用状态，因此$A$和$B$未连接。当$EN = 1$且$\overline{EN} = 0$时，传输门处于打开或启用状态，任何逻辑值都可以在$A$和$B$之间流动。

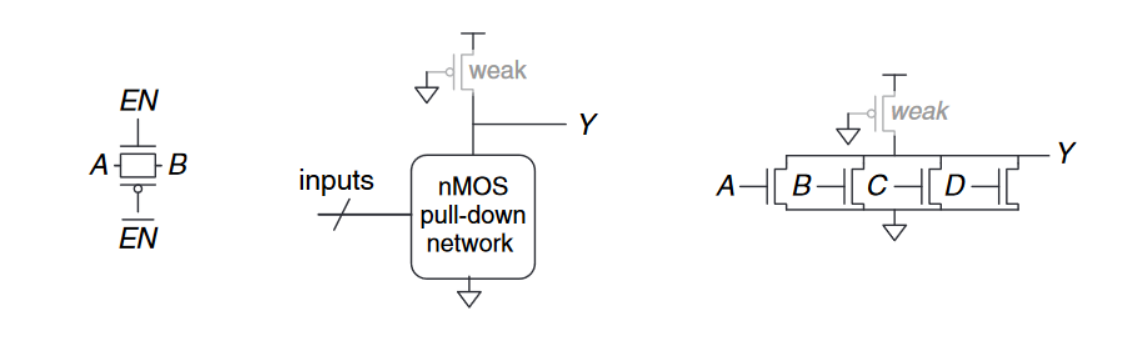
transimission gate and pseudo nMOS

Pseudo-nMOS Logic

一个$N$输入的$CMOS$非门使用$N$个$nMOS$晶体管并联和$N$个$pMOS$晶体管串联。事实上，串联的晶体管的速度会比并联的晶体管速度慢，因为串联的电阻比并联的电阻阻值更大。不仅如此，由于空穴并不能像自由电子一样快速地在硅晶格周围移动，因此$pMOS$的速度也比$nMOS$的速度慢。这样下来，并联的$nMOS$是要比串联的$pMOS$速度更快的，尤其是当许多晶体管串联时。

因此，我们就引入了伪-$nMOS$逻辑(pseudo-nMOS logic)，用一个始终处于开启状态的单个弱$pMOS$(week $pMOS$)晶体管来代替一组速度较慢的$pMOS$晶体管，如上图中的中间图例所示。这个$pMOS$晶体管通常被称为弱上拉(week pulled-up)。由于被选择的$pMOS$尺寸的物理特性，使得其微弱地将输出$Y$拉高，即仅当没有任何$nMOS$晶体管处于导通时，该弱上拉会使得输出$Y$产生逻辑1。但是，一旦有任何一个$nMOS$晶体管处于导通状态，其就会压倒弱上拉将输出$Y$拉低至产生逻辑0。

伪$nMOS$逻辑的优势在于可以用于构建多输入的快速异或门，例如上图中的有图所示。更多的优势我们将在后续的笔记中描述。而其缺点是当输出为低电平时，$V_{DD}$和$GND$之间存在短路；弱$pMOS$和$nMOS$晶体管都会处于导通状态，这种短路会持续的吸收功耗，应当谨慎使用。

值得注意的是：伪$nMOS$逻辑的出现主要是因为$nMOS$晶体管在早期的工艺中比$pMOS$晶体管易于实现和快速。在早期的集成电路设计中，$nMOS$晶体管比$pMOS$晶体管更容易制造，并且具有更高的工作速度和更低的功耗。因此，工程师们采用了伪$nMOS$逻辑设计来构建数字逻辑电路。伪$nMOS$逻辑电路使用$nMOS$晶体管作为开关，而$pMOS$晶体管仅用于电路的拉高操作，从而提高了电路的速度和性能。
虽然$pMOS$晶体管的速度相对较慢是一种因素，但并非是伪$nMOS$逻辑出现的唯一原因。

Power Consumption

功耗(power consumption)是单位时间内所消耗的能源量。在现代架构中，如何减少功耗是一个巨大的难题，同时也在数字系统中占据了非常重要的地位。

数字系统会同时消耗动态功率(dynamic power)和静态功率(static power)。动态功率是在信号0和1之间变化时用于充电电容的功率；静态功率是即使在信号未发生变化或系统处于空闲状态时也会消耗的功率。

逻辑门极其连接它们的导线具有电容。从电源抽出能量为电容$C$充电至电压$V_{DD}$的能量是$CV_{DD}^2$。如果电容器上的电压以频率$f$(即每秒$f$次)切换，则每秒它充电$f/2$次和放电$f/2$次。放电不会从电源中消耗能力，因此动态功耗为：

$$
P_{dynamic} = \frac{1}{2}CV_{DD}^2f
$$

电子系统即使在空闲时也会吸收一些电流。当晶体管关闭时，它们会泄漏小部分电流，比如上一节讨论的伪$nMOS$门，有一条从$V_{DD}$到$GND$的通路，通过该路径电流持续流动。总静态电流$I_{DD}$也被称为泄漏电流(leakage current)或静态电源电流(quiescent supply current)，其流动在$V_{DD}$和$GND$之间。静态功耗与这个静态电流成正比：

$$
P_{static} = I_{DD}V_{DD}
$$

Summary

本篇笔记介绍了一些理解和设计复杂系统的基本原理，逻辑门通常由$CMOS$晶体管构成，其表现为电控开关。$nMOS$在栅极为1时导通，而$pMOS$在栅极为0时导通。