Combinational Logic Design

在上一篇笔记中，我们已经学习了关于数字系统的一些基本原理以及构建和理解数字系统的基本概念。现在本篇笔记将讲解组合逻辑(Combinational Logic)，即输出只取决于当前的输入。在上一篇笔记中的逻辑门介绍都是组合逻辑的例子，本篇中你将学习设计多个门电路，以实现由真值表(truth table)或布尔方程(Boolean Equation)指定的输入和输出之间的关系。

Introduction

在一个数字电子学中，电路(circuit)是处理离散变量的网格，其可以被看作一个黑箱，如下图中左图所示：

  • 一个或多个离散值输入接口
  • 一个或多个离散值输出接口
  • 描述输入和输出之间关系的功能规范(functional specification)
  • 描述输入变化和输出相应之间延迟的时许规范(timing specification)

black box with circuit

电路由节点(node)和元件(element)组成。一个元件本身就是一个具有输入输出和规范的电路；节点是导线，其电压传递一个离散值变量。节点一般分为输入、输出和内部节点(也就是没有输入或输出的导线)。上图中的左图解释了三个元件的电路，以及六个节点。

数字电路被分为组合逻辑电路或时序逻辑电路(sequential)。一个组合逻辑电路的输出只取决于输入的当前值；时序逻辑电路的输出则取决于输入的当前值和之前的值(也就是上一个状态)，换句话说，其取决于输入的序列。组合逻辑是无记忆性(memoryless)，而时序逻辑是具有记忆性(memory)。

组合电路的功能规范用电流输入值表示输出值，时序规范由输入到输出的上界和下界组成。我们首先关注的功能规范。

下图展示了一个二输入单输出的组合电路，黑盒内部的符号℄表明它只用组合逻辑实现，在下图的例子中，特指功能$F$为$OR$：$Y = F(A, B) = A + B$。同时，我们也可以从右图中发现，对于单个功能的实现可能会存在多种形式，在给定可用的构建块和设计约束下，可以自由地选择如何设计。

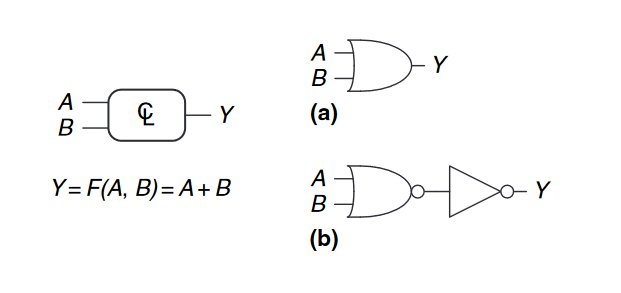
combinational logic circuit

而下面一张图则表示了多输出的情况，该电路被称为全加器(full adder)。为了简化图纸，我们通常使用一条带斜线的单线和旁边的一个数字来表示总线，即多个信号的约束。该数字规定了总线中有多少个信号。如下图中的左图所示。如果位数不重要或上下文中明显，就可能如图b一样只展示斜线，不表示数字，表示一个块的任意数量的输出作为第二个块的输入。

multiple-output

而组合构图(combinational composition)的规则告诉我们如何从较小的组合逻辑电路元件构造一个大的组合电路：

  • 每个电路元件本身就是组合的
  • 电路的每个节点要么被指定为电路的输入，要么恰好连接电路元件的一个输出端
  • 电路中不包含循环路径：每条经过电路的路径至多访问每个电路节点一次。

大型电路(比如微处理器)是非常复杂的，所以我们使用从上一篇笔记中所说的原则来管理复杂性。将电路看成一个具有良好定义的接口和功能的黑盒，是抽象化和模块化的运用；由小模块构建电路是层次化的应用；而组合构图则是规约的一种运用。

Boolean Equations

布尔方程(Boolean Equations)处理的变量要么为$TRUE$，要么为$FALSE$，因此它们非常适合描述数字逻辑。本节定义了布尔方程中常用的一些术语，然后展示了如何根据真值表为任何逻辑函数编写布尔方程。

Terminology

变量$A$的补(complement)被称为$\overline {A}$。一个变量或自身的补被称为字面量(literal)。我们也称$A$是变量的真正形式(true form)，而$\overline {A}$是变量的补充形式(complementary form)。真正形式并不意味着$A$就是$TRUE$，仅仅是说明$A$没有上划线。

一个或多个字面量的$AND$运算被称为乘积(product)或蕴含项(implicant)。一个最小项(minterm)是一个涉及到函数的所有输入的积；一个最大项(maxterm)是一个涉及到函数的所有输入的和。

Sum-of-Products Form

一个$N$输入的真值表包含$2^N$行，真值表中的每一行都与一个最小项相关联，而该最小项就是该行的$TRUE$值。例如下图中的左图所示，第一行的最小项是$\overline {AB}$，因为当$A = 0, B = 0$时，$\overline {AB} = TRUE$。最小项的编号从0开始计算。

truth table and minterms

对于任意一个真值表，我们可以通过求和每一个最小项来写出一个布尔方程，其满足输出$Y = TRUE$即可。比如上图中两表画蓝圈所表示的：$Y_1 = m_1 = \overline {A}B$，$Y_2 = m_1 + m_3 = \overline {A}B + AB$。

如上述的表达式被称为函数的乘积和规范式(sum-of-products canonical form)。其表明了，对于同一个真值表，我们总是能够写出相同的布尔表达式(即真值表具有唯一性)。乘积和规范式也可以使用求和符号$\sum$写成sigma表示法(sigma notation)：

$$
F(A, B) = \sum(m_1, m_3) or F(A, B) = \sum(1, 3)
$$

同时，乘积和规范式为任意变量个数的真值表提供了一个布尔方程。但令人遗憾地是，乘积和规范式并不一定产生最简单的方程。产生最简式的方法将在后续介绍。

Product-of-Sums Form

布尔表达式的另一种表示方式是和积规范式(product-of-sums canonical form)。真值表中的每一行都与一个最大值相关联，而该最大值就是该行的$FALSE$值。对于任意一个真值表，我们可以通过乘积每一个最大项来写出一个布尔方程，其满足输出$Y = FALSE$即可。和积规范式也可以使用乘积分号$\Pi$来表示pi表示法(pi notation)。

只有当少数几行真值表上的输出为$TRUE$时，乘积和规范式产生一个较短的等式；仅当少数几行真值表上的输出为$FALSE$时，和积规范式更简单。

Boolean Algebra

为了产生最简式，我们可以通过布尔代数(Boolean Algebra)来简化布尔方程。布尔代数的规则与普通代数的规则非常类似，并且在某些情况下更为简单。

布尔代数的公理和定理都遵循对偶原则(the principle of duality)。如果符号0和1以及$+$和$\cdot$可以互换，并且语句依旧正确，那么就可以使用$\prime$来标记一个语句的对偶。

Axioms

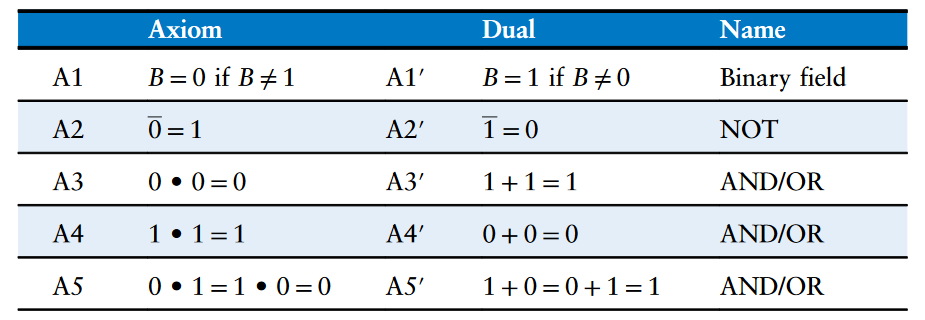
下表陈述了布尔代数的公理(Axioms)。这五条公理和它们的对偶定义了布尔变量和$NOT$、$AND$和$OR$。

Axioms of Boolean Algebra

Theorems of One Variable

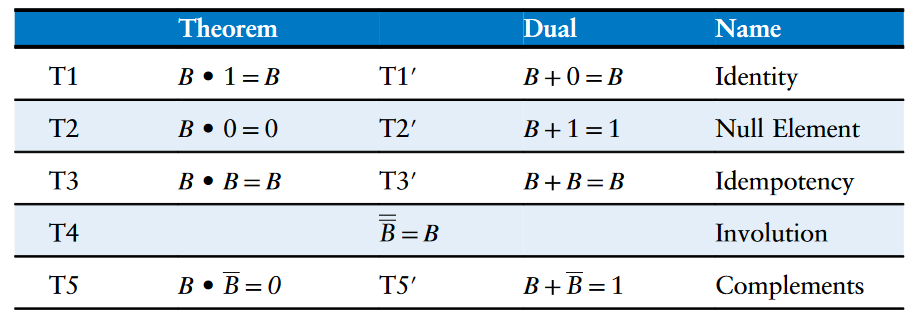
下表陈述了布尔代数的定理(Theorems)。这五条定理描述了如何化简含有一个变量的方程。

Boolean theorems of one variable

Theorems of Several Variables

下表描述了如何简化多个布尔变量。

Boolean theorems of several variables

从德摩根律可以得出一些有趣的结论。假如我们把反转圈(inversion circle)看作气泡(bubble)，如果你把下图中在输入端的“气泡”推向输出端，那么输入端的“气泡”就会移动到输出端，然后门体就会发生翻转(比如从$OR$翻转为$AND$)，我们就得到两个不同的逻辑门表示同一个门功能。但是，“气泡”的推动是有一些依赖规则的：

  • 向前或向后(输入到输入为向前)推动“气泡”会改变门体从$AND$到$OR$，反之亦然
  • 从输出端推回“气泡”会使得输入端的每个接口都会有一个“气泡”
  • 保证输入端都有“气泡”的情况下，从输出入段推送“气泡”会使得输出端有一个“气泡”

De Morgan equivalent

Simplifying Equations

简化乘积和规范式的基本原理是利用关系式$PA + P\overline{A} = P$来组合项，其中$P$可以是任意蕴含项。我们定义一个乘积和规范式如果在尽可能少的使用蕴含项的情况下那么就是最小化方程(minimized)。如果有几个方程具有相同的蕴含项，则最小的则是具体字面量少的那个。

如果一个蕴含项不能与方程中的其他任何蕴含项结合起来，以较少的字面量构成一个新的蕴含项，就称其为素蕴含项(prime implicant)。最小化等式中的蕴含项一定都是素蕴含项。

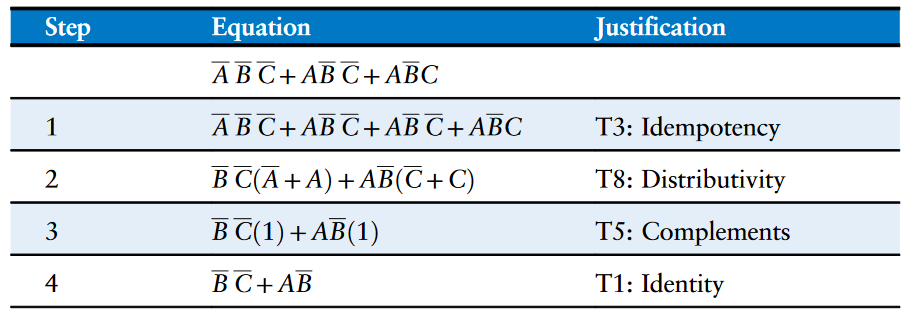
improved equation

如上图所示，虽然这有点反直觉($A\overline{B}C = A\overline{B}C + A\overline{B}\overline{C}$)，但扩展蕴含项有时在简化最小化方程时有妙用。这样做能够重复扩展的最小项中的一个与另外一个最小项进行组合。

或许你已经注意到，使用布尔定理完全简化一个布尔代数方程可能会导致一些错误的(也就是求出来的最小化可能有误)。后续笔者会介绍另一个被称为卡诺图的方法，用于简化。

From Logic To Gates

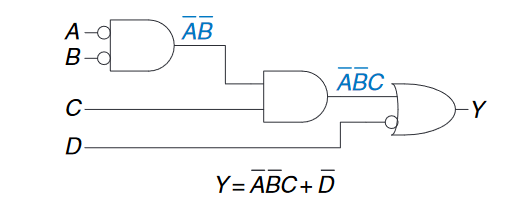
原理图(schematic)是数字电路的示意图，显示了连接它们的元件和导线。比如该等式$Y = \overline{A}\overline{B}\overline{C} + A\overline{B}\overline{C} + A\overline{B}C$可能的硬件实现为：

schematic

通过一致的方式绘制原理图使得它们更容易阅读和调试，以下是一些准则：

  • 原理图中的输入通常是在左边(或上方)
  • 原理图中的输出通常是在右边(或下方)
  • 在可能的情况下，门应该是从左到右的
  • 直线导线比有多个拐角的导线更好用(参差不齐的导线会浪费精力跟踪电线，而不是思考电路的功能)
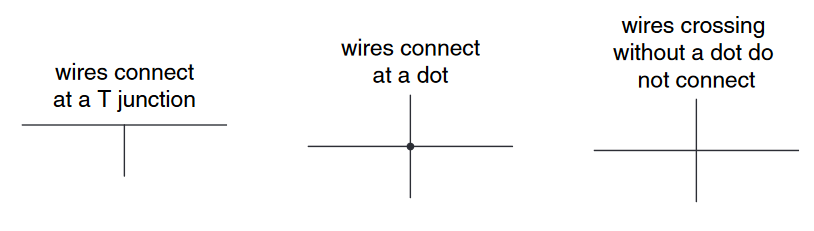
  • 导线总是连接在$T$连结上
  • 导线交叉的点表示导线之间的连接(若无点，则说明不连接)

wires form

任何乘积和规范的布尔方程都能够用系统的方式绘制成原理图。可编辑逻辑阵列(Programmable Logic Array，PLA)是一种数字电路，其中包含了一系列可编程的逻辑门，允许用户根据特定需求配置逻辑功能。$PLA$通常由一组可编程的$AND$门阵列和一组可编程的$OR$门阵列组成。通过编程这些门的连接方式和输入，可以实现各种逻辑功能，从而定制化地构建数字电路。

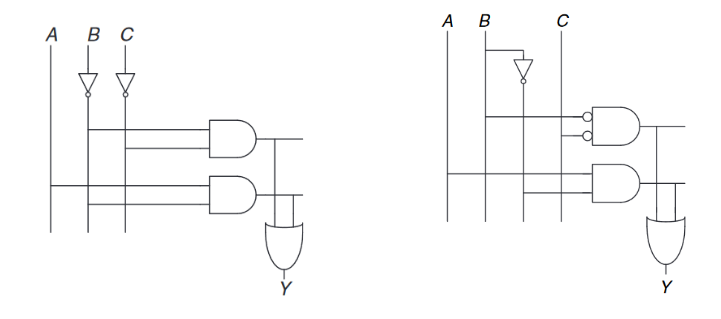
我们可以利用非门来进一步减少门的数量，比如下图中$\overline{B}\overline{C}$是一个带反向输入的与门。我们回忆以下德摩根律，一个带反向输入的与门等价于一个或非门。根据实现的技术不同，使用最少的门或优先使用某些类型的门或许更便宜，这样我们就能够再次进行优化。

optimization gate

许多电路具有多个输出，其每个输出都与单独的布尔函数输入相关。我们可以为每个输出写一个单独的真值表，但在单个真值表上写出所有的输出，并用所有的输出画出一个示意图往往是方便很多的。例如，四输入优先电路的绘制：

  • 当$A_3$是导通时，$Y_3$才能是$TRUE$，因此$Y_3 = A_3$
  • 当$A_2$是导通的，$A_3$断开时，$Y_2$才能是$TRUE$，因此$Y_2 = \overline{A_3}A_2$
  • 依次类推…$Y_1 = \overline{A_3}\overline{A_2}A_1$，$Y_0 = \overline{A_3}\overline{A_2}\overline{A_1}A_0$
  • 然后列出四个输出的真值表
  • 画出对应电路

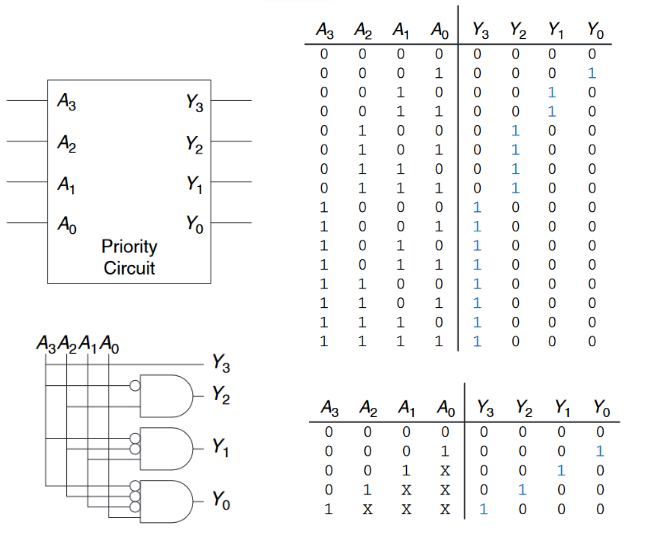
priority circuit

我们需要注意的是，当$A_3$是导通时，该优先电路的输出不关心其他的输入是什么，因此，我们使用$X$来描述不被输出关心的输入值。然后，我们可以简化该真值表，如上图所示。

Multilevel Combinational Logic

在乘积和规范式的逻辑被称为二级逻辑(two-level logic)，因为它由字面量连接到一级与门和一级或门。通常的，我们使用多级组合逻辑来设计电路，因为其可能使用更少的元件。

Hardware Reduction

现在我们学过的异或门来看，假如我们想要通过二级逻辑来构建三输入的异或门。

回忆$N$输入异或门：当有奇数个输入为$TRUE$时，异或门的输出是$TRUE$。因此我们得到其表达式：$Y = \overline {A}\overline {B}C + \overline {A}B\overline {C} + A\overline {B}\overline {C} + ABC$。我们发现，该表达式已经没有办法再简化了。

另一方面，$A \oplus B \oplus C = (A \oplus B) \oplus C$，因此，三输入异或可以由二输入的异或级联而成。

依次推广，你会发现使用二输入的异或级联称为多输入的异或是极好的，假如你需要一个个三输入异或，你就需要$128$个输入的或门和$128$个八输入与门级联。不过，选择一个特定逻辑功能的最佳多级实现不是一个简单的过程。

Bubble Pushing

$CMOS$更倾向于使用与非门和或非门(而非与门和或门)。但是，通过观察具有与非门和或非门的多级电路来构建方程是一件非常复杂的事。所以“气泡”的推动有助于重绘这些电路，以便“气泡”消除和功能更容易确定。

  • 从电路的输出端开始，向输入端工作
  • 推回任何再最终输出上的“气泡”使得你可以根据输出读取一个方程(也就是输出$Y$而不是$\overline {Y}$)
  • 往后回推，绘制每个门的形式以至于“气泡”抵消：
    • 如果当前门有一个输入“气泡”，那么前一个门(注意，前一个门是指从右往左方向)就应该有一个输出“气泡”
    • 如果当前门有一个输出“气泡”，那么后一个门就应该有一个输入“气泡”

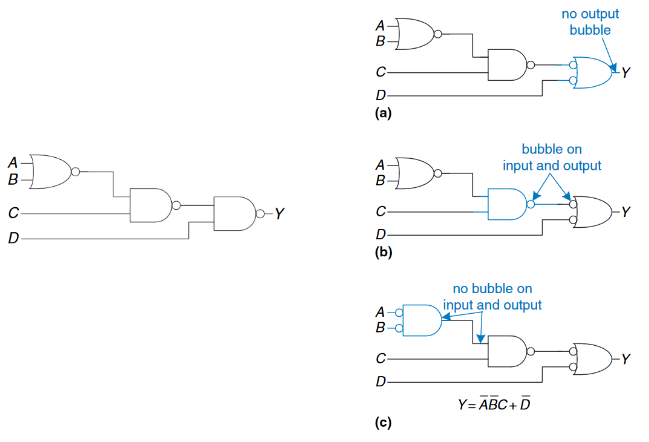
bubble-pushed circuit

最后需要强调的是，由于串联的气泡相互抵消，我们可以忽略在中间门的输出和最右门的一个输入上的“气泡”，因此得到：

Logically equivalent bubble-pushed circuit

X’s and Z’s, Oh My

虽然布尔代数限制在0和1之间，但是真实的电路会存在非法值和浮动值，使用$X$和$Z$分别代替。

Illegal Value: X

符号$X$表示电路节点存在未知的(unknown)或非法的(illegal)值，其通常发生在电路同时导通0和1，这种情况被称为竞争(contention)。这种情况的发生是被错误的且必须避免的。发生竞争后，该电路节点的电压通常是在$0 \thicksim V_{DD}$的，并且绝大多数都是在禁区的。竞争会导致大量电能在冲突的门中流动，导致电路发热并损坏。

$X$值也通常被用于电路模拟中的未初始化值。不过，回忆之前看的，我们在真值表中也会出现$X$，但是该$X$与这两种情况不同，仅仅是表示其值可以被忽略的。

Floating Value: Z

符号$Z$表示一个节点既不在高电压也不在低电压，因此被称为浮动(floating)、高阻抗(high impedance)或者高Z(high Z)。一个经典错误是：浮动或非驱动的节点的逻辑值和0相同；实际上，浮动节点可能为0也可能为1，还可能为其中间的其他电压值，这取决于系统。还需要注意的是：一个浮动的节点所表现的电路状态不总是错的，有可能也会正确的执行其功能。

产生浮动节点的一种常见方式是：忘记将电压接到电源输入，或假设未连接的输入与取值为0的输入相同。这种错误就可能导致当浮动值在$0 \thicksim 1$随机变化时，电路表现出不规律。

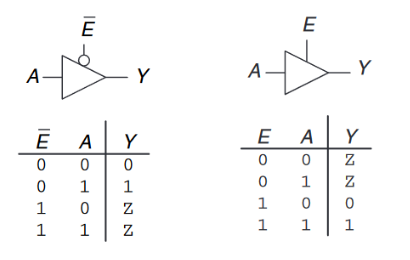
tristate buffer

三态缓冲器(tristate buffer)有三种可能的输出状态：HIGH(1)、LOW(0)和floating(Z)。当使能$E$表现不同状态时，三态缓冲器的输出也会随之变化。三态缓冲器常用于在总线上连接多个芯片。

比如说微处理器、视频控制器和以太网控制器都需要与计算机中的存储系统通信，每个芯片都可以通过使用三态缓冲器连接到一个共享内存总线上。同时，该共享总线一次性只能与一个控制器通信，因此其他控制器就必须进入浮动输出状态以免干扰通信中的控制器。不过在现代计算机中，点对点链路可以实现更高的通信速度，芯片之间直接连通，不再通过总线共享。

Karnaugh Maps

在使用布尔代数对布尔方程进行多次最小化后，你会意识到，一旦你不小心，最后就会得到一个完全不同的方程，而不是一个简化的方程。因此，卡诺图(Karnaugh maps, K-maps)时一种简化布尔方程的图解方法。卡诺图善于处理至多四个变量的情况。

回想一下，逻辑最小化涉及到组合项：将包含一个蕴含项$P$的两项与某一变量$A$的真实形式和互补形式组合，以消除$A$，即$PA + P\overline{A} = P$。卡诺图以图解的形式展示出来。

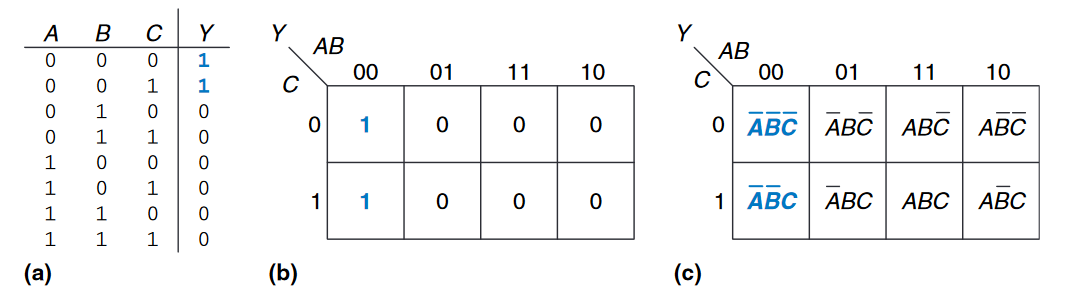
下图展示了真值表和卡诺图。卡诺图的最上面的行给出了输入$AB$的四个可能值，左边的列给出了输入$C$的两个可能值。每一个正方形格都对应着真值表中的一行，并且包含该行的输出$Y$的值。图(c)显示了卡诺图中的每个正方形格对应的最小项。

每个单元格(或最小项)因单个变量的变化而与相邻的单元格不同，意味着相邻的单元格共享除一个以外的所有相同的字面量(也就是$\overline{A}\overline{B}\overline{C} \longrightarrow \overline{A}B\overline{C}$, $\overline{A}\overline{B}\overline{C} \longrightarrow \overline{A}\overline{B}C$等等)。你或许注意到，顶部$AB$的取值是特殊的：$00,\ 01,\ 11,\ 10$，这不同于正常顺序的二进制编码，而是格雷码(Gray code)。也就是说，相邻元素只有单个值发生变化，不会有多个值同时变化。

卡诺图是“环绕的”：最右边的列与最左边的列是有效相邻的(变化同样是单元素变化)，也就是说，可以将卡诺图卷成一个圆柱体，端点连接成为圆环，保证性质不变。

Three-input function

Circular Thinking

在上图中，只有两个最小项，而从卡诺图中读取最小项恰好等价于直接从真值表中读取乘积和规范式。

在这之前，我们可以通过布尔代数得到最小化：

$$
Y = \overline{A}\overline{B}\overline{C} + \overline{A}\overline{B}C = \overline{A}\overline{B}(\overline{C} + C) = \overline {AB}
$$

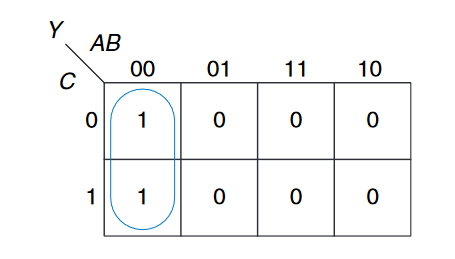
现在，卡诺图可以通过圈住邻近值为1的单元格帮助我们图像化地简化。

对于每个圈，我们应该写出对应的蕴含项(重温一下，蕴含项是一个或多个字面量的组合)。但是记住真值形式和互补形式都在圈内的变量将被排除在蕴含项之外。

K-maps minization

Logic Minimization with K-Maps

卡诺图提供了一种简易的可视化方法来得到最小化。只需要使用尽可能少的圆圈数，将地图中的表示1值的所有单元格圈出即可。更为正式地说，当一个布尔方程被写成最少的素蕴含项的和时，是最小化的；因此卡诺图上的每个圆圈代表一个蕴含项，最大可能的圆圈为素蕴含项。

这里给出从卡诺图中找到最小化的规则：

  • 使用最少且必要的圈来覆盖所有的1
  • 圈内的所有单元格都必须包含1
  • 每个圈必须跨越一个矩形块(该矩形块必须是$1、2、4$个方格组成的)
  • 每个圆圈必须尽可能的大
  • 圆圈必须在卡诺图的边界内
  • 如果允许使用较少的圆，则卡诺图中的一个1可以被循环多次包含

一个七段数码管解码器接受一个四位数据输入$D_{3:0}$，并产生七个输出来控制发光二极管以显示从0到9的数字。这七个输出通常称为$a$到$g$段，或者$S_a–S_g$，如下图所定义。数字如下图所示。编写输出的真值表，并使用卡诺图找到$S_a$和$S_b$的布尔方程。假设非法的输入值$(10–15)$会产生一个空白输出。

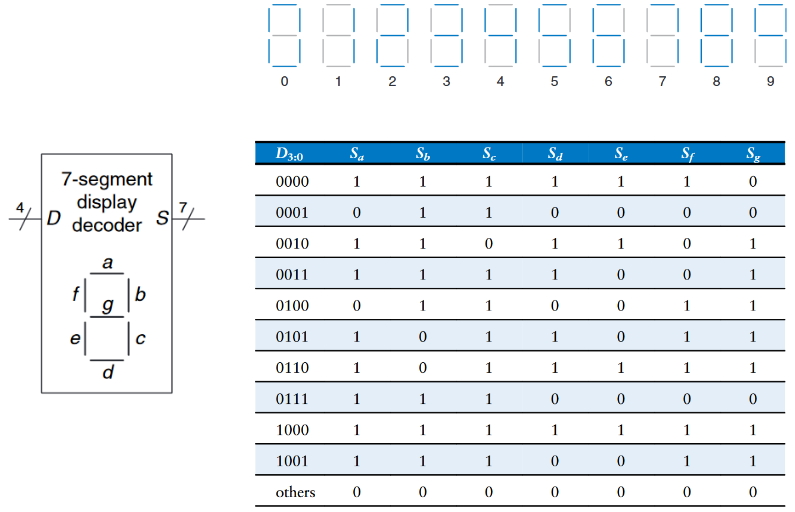
Seven-digit truth table

其$S_a - S_g$的真值表如上图所示，而$S_a$和$S_b$的卡诺图如下所示。然后我们将所有相邻的1按照卡诺图的规则尽可能多的圈出来，就得到了最下方的卡诺图。

K-Map solution

需要注意：素蕴含项的最小化集合并不唯一。比如说，$S_a$的卡诺图中的$0000$项与$1000$项可以共同产生出$\overline{D_2}\overline{D_1}\overline{D_0}$，可也能和$0010$项产生出$\overline{D_3}\overline{D_2}\overline{D_0}$。

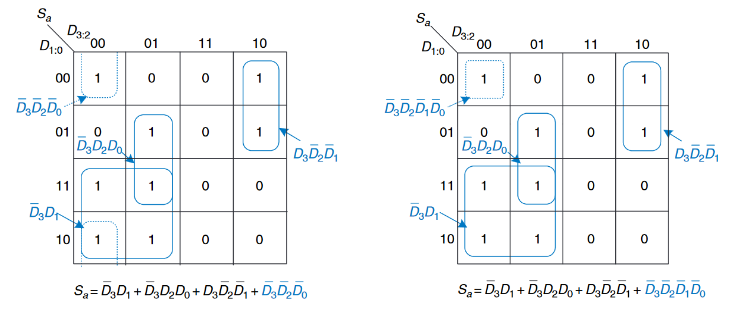
alternative K-maps for Sa

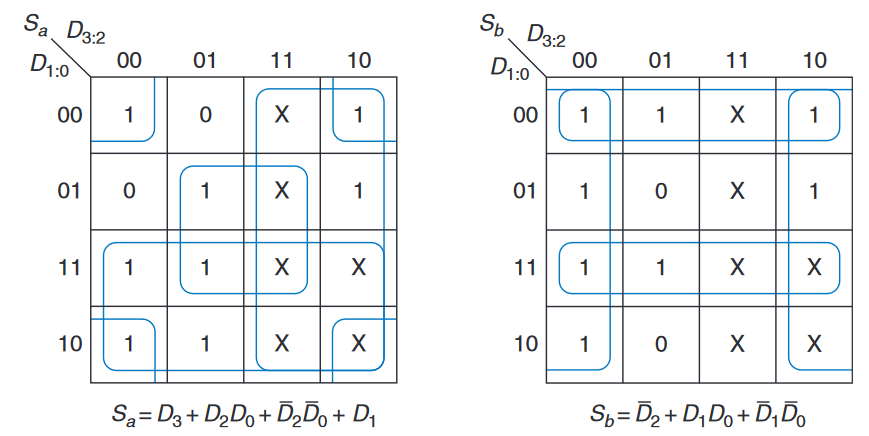
上图中的右图需要注意：这里出现了一个常见的错误，即在左上角选择了一个非素蕴含项来覆盖1。这个最小项$\overline{D_3}\overline{D_2}\overline{D_1}\overline{D_0}$给出了一个不为最小化的乘积和规范式。该最小项可以和相邻的任意一个项组合形成一个更大的圆圈。

Don’t Cares

回忆我们在之前学习的$X$，即真值表的输入不被输出所关心。这一概念其实也能出现在真值表中输出不被输入所关心。因此，在卡诺图中，$X$允许进一步逻辑最小化，如果被圈出的对圈没有任何帮助，那么是可以被忽略的。

K-Maps with don't cares

The Big Picture

卡诺图和布尔代数都是为了寻找到一种低成本实现特定逻辑功能的方法。但在现代工程实践中，通过逻辑综合器的计算机程序可以从逻辑函数的描述中生成最简电路，因此对于大型问题，使用逻辑综合器更佳。我们将在后续进行学习。

Combinational Building Blocks

组合逻辑通常被组合成一个更大块来构建更为复杂的系统。这是一种抽象原则的应用，隐藏了不必要的门级细节以强调组成块的功能。本节中会介绍多路复用器(multiplexer)和解码器(decoders)。

Multiplexer

多路复用器(Multiplexer)是最常用的组合电路。其根据一个选择信号的值从多个可能的输入中选择一个输出。多路复用器又被称作mux。

2:1 Multiplexer

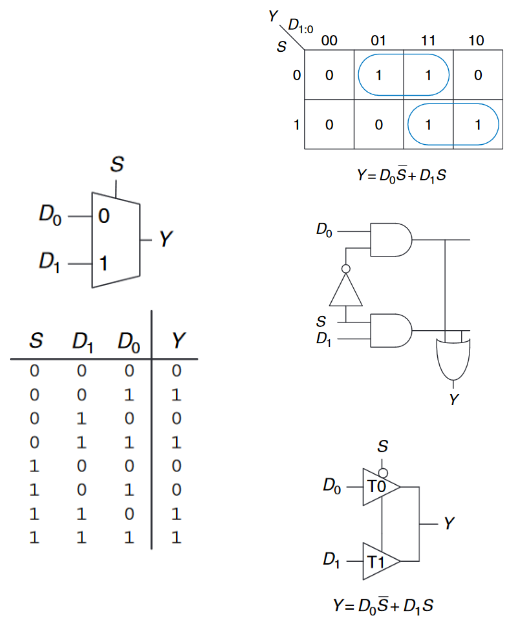
下图展示了2:1多路复用器的原理图和真值表。其有两个输入$D_0$和$D_1$，一个选择输入$S$以及一个输出$Y$。其遵循：当$S=0$时，$Y=D_0$反之则$Y=D_1$。$S$也被称为控制信号(control signal)。

其有图展示了2:1多路复用器的卡诺图和逻辑电路。当然，我们还有另一种方式构建多路复用器，也就是通过三态缓冲器。三态缓冲器使得在任何时候，只有一个三态缓冲器是激活的，当$S = 0$时激活三态$T_0$，反之激活$T_1$，就能够实现同等功能。

2:1 Multiplexer

Wider Multiplexer

下图展示了4:1多路复用器，我们可以发现，多路复用器可以有三种构成方式：与门、三台缓冲器和多路复用器级联。我们也可以发现，如果在更大的多路复用器上，其控制信号的个数为$\log_2N$，并且依旧能使用这三种方式来构建。

4:1 Multiplexer

Multiplexer Logic

多路复用器可以使用查找表(lookup tables)的方式来实现逻辑功能。

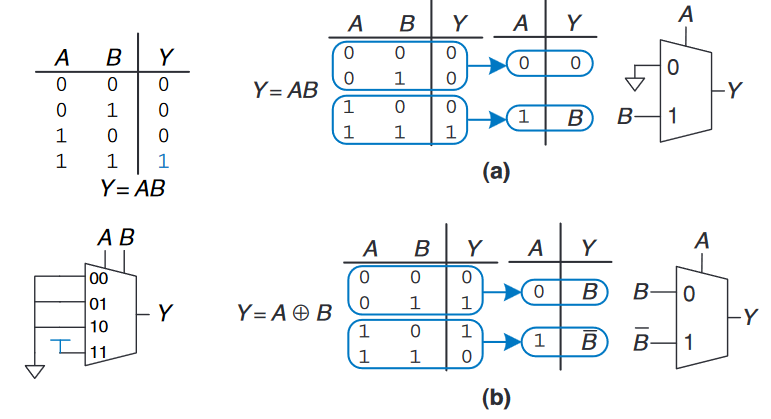
下图使用了4:1多路复用器来实现二输入与门的逻辑操作.实际上，对于任意一个$N$输入的逻辑函数，其都可以被$2^N$个输入的多路复用器来实现。其方法是：写出逻辑函数的真值表，通过真值表的值对多路复用器的输入进行连接，而对应的输入作为多路复用器的控制信号用以查找表即可。

multiplexer logic implement

Decoders

一个解码器(decoder)有$N$个输入和$2^N$个输出。它的每一位输出都依赖于输入的组合。下图是2:4解码器的逻辑，其输出被称为独热(one-hot)，因为在给定条件下一次只有一个输出为hot(HIGH)状态。

解码器和译码器这两个术语是等同的

译码器的每一个输出都依赖于所有输入的真实形式或互补形式。总之，一个$N:2^N$译码器可以由$2^N$个输入与门通过接收所有输入的$TRUE$或$FALSE$的各种组合值构成。译码器的每一个输出都表示了一个最小项。

Decoder implement

Decoder Logic

译码器可以与或门一起来构建逻辑函数。如上图所示，一个2:4译码器与一个二输入或门构建了一个二输入同或门$Y = AB + \overline{AB} = \overline {A \oplus B}$。

使用译码器来构建逻辑电路时，很容易将函数表示成真值表或乘积和规范式。一个在真值表中有$M$个1的$N$输入函数能够被一个$N:2^N$译码器和一个$M$个输入的或门连接所有输出1的最小项构成。这在后面的只读存储器中会被使用。

这里看起来或许比较晦涩拗口，所以给出一个小例子：
假如你需要实现二输入的与门，我们已经知道其真值表中有一个输出为1。因此选择2:4译码器和一个一输入或门(也就是说，二输入或门的一个输入永远是0)，然后根据二输入与门的真值表可知，只有两个输入同时为1时，输出才为1，那么我们选择2:4译码器中的Y_3，然后连接所有最小项，可以得到其方程$Y = Y_3 + 0 = AB + 0 = AB$
这样就得到了通过2:4译码器和一个一输入或门实现二输入与门的实现

Timing

在之前的几个小节中，我们主要关注理想状况下使用最少数量的门的电路工作情况。实际上，电路设计中最具挑战的问题之一是时序问题：如何使电路运行地更快。

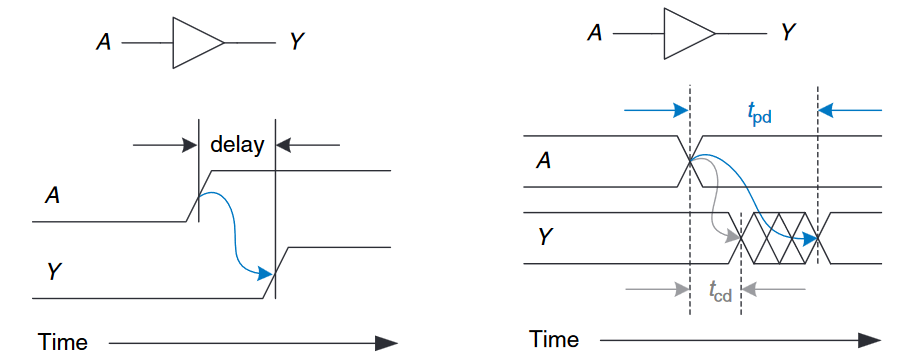
一个输出需要时间来响应一个输入的变化。下图展示了缓冲器的输入变化和后续输出变化之间的延迟(delay)。这种图被称为$时序图(timing diagram)$；它刻画了当输入变化时缓冲电路的瞬态响应(transient response)。从$LOW$到$HIGH$的转变被称为上升沿(rising edge)，当然，从$HIGH$到$LOW$的变化被称为$下降沿(falling edge)$。蓝色的箭头表示了$Y$的上升沿是由于$A$的上升沿引起的。我们在输入信号$A$的$50%$点与输出信号$Y$的$50%$点测量延迟。50%点(50% point)是信号在转变过程中电压处于高电平和低电平之间中间点(half-way)的值。

Circuit delay

Propagation amd Contamination Delay

组合逻辑电路的时序特征是传播延时(Propagation Delay)和污染延时(Contamination Delay)。传播延时$t_{pd}$是指输入发生变化直到输出或输出到达到其最终值的最长时间；而污染延时$t_{cd}$是指输入发生变化直到输出开始变化其值的最小时间。

如上图所示，缓冲器的传播延时和污染延时分别由蓝色和灰色表示。上图表示了$A$的初态要么是$HIGH$要么是$LOW$，并在特定时间变化到另一种状态。我们并不关心其值，只对其发生了变化进行关注。$Y$在$A$改变一段时间后才会响应。弧线表示$Y$可能在$A$转变后$t_{cd}$时间后开始相应，在$t_{pd}$时间内会稳定到新值。

电路延迟的根本原因包括电路中电容充电的所需时间和电信号以光速传播，为此，$t_{cd}$和$t_{pd}$不同的可能原因为：

  • 不同的上升和下降延迟
  • 多个输入和输出之间的延迟可能不同
  • 电路在冷时加速，热时减速

想要详细准确地计算$t_{cd}$和$t_{pd}$需要深入到更低的抽象层次，这不在我们的研究范围。然而，制造商通常会提供数据表来指定每个门的延迟。

如前所述，传播延时和污染延时也和信号从输入到输出的路径决定。

下图展示了一个四输入逻辑电路。蓝色表示的是关键路径(critical path)，其是最长的同时也是最慢的一条路径，因为输入通过了三个门才传输到输出。这条路径是关键路径的原因是因为它限制了电路的运行速度。灰色表示的是最短路径(short path)，其只从输入到输出经过一个门，所以是最短的路径也是最快的路径。

Critical and short path waveforms

组合逻辑电路上的传播时延是在关键路径上的每一个元件的传输延迟之和。污染时延是最短路径上每个元件的最小延迟之和。比如上图中的时延为：

$$
t_{pd} = 2t_{pd_AND} + t_{pd_OR}
$$

$$
t_{cd} = t_{cd_AND}
$$

Glitches

至今为止，我们只讨论了单输入转换导致单输出转换的情况。然而，单个输入转换可能导致多个输出变换，这被称为毛刺(glitches)或危险(hazards)。尽管永昌毛刺不会造成问题，但是重要的是要意识到它们的存在，并在查看时序图时识别出它们。

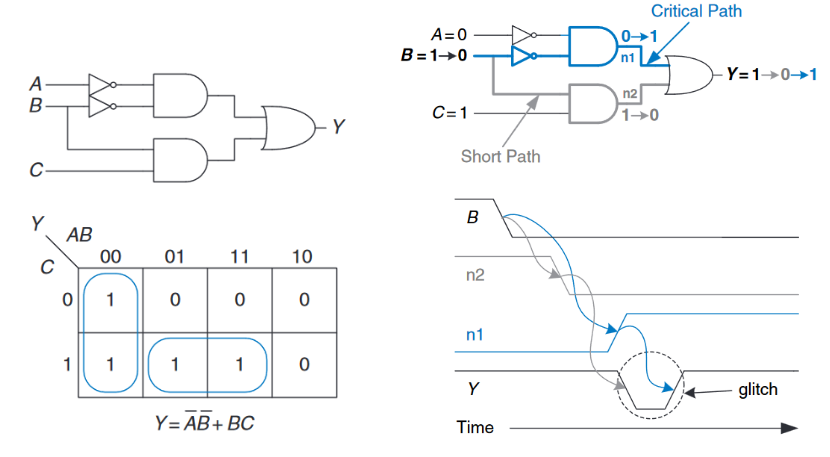
Circuits with a glitch

上图表示了一个带有毛刺电路的卡诺图和电路。最短路径(用灰色表示)穿过两个门，与门和或门。关键路径(用蓝色表示)穿过三个门，非门，与门和或门。当$B$从1跃迁到0时，$n2$(在短路径上)先于$n1$(在关键路径上)下降。直到$n1$上升前，或门的两个输出都是是0，使得输出$Y$跌至0。当$n1$最终上升后，$Y$才会回到1。上图中也展示了该状况的时序图，$Y$从1开始变化，以1结束，但是在中间暂时产生了毛刺0。

因此，只要我们在读取输出之前的等待时间和传输延迟一样长，毛刺的出现就不会造成问题，因为输出最终将稳定在正确的值。

添加另一个逻辑门可以避免这样的毛刺。下图中的卡诺图可以解释这一问题，我们发现从$ABC = 001 \longrightarrow ABC = 011$的过程正好是上述$B$发生变换的过程，也就是其产生了一个毛刺。因此，卡诺图中跨越两个素蕴含项边界的跃迁预示着一个可能的毛刺。

由上图中的时序图可以看出，如果一个素蕴含项的电路在另一个素蕴含项的电路开启之前关闭，就会产生毛刺。为了去除毛刺，可以增加一个新的覆盖该蕴含项边缘的圆圈，根据一致性定理，新增加的项$\overline{A}C$是一致的或冗余的。

Circuit without glitch

上图就表示了一个无毛刺的电路。增加了一个与门(蓝色高亮部分)，此时，$B$的跃迁不再导致输出的毛刺产生，因为这个与门在整个转移过程中输出1。

总之，当单个变量的跃迁导致卡诺图中的两个素蕴含项之间的边界被跨越时，我们能够通过在卡诺图中增加多余的蕴含项来消除毛刺。但这会带来额外的硬件成本代价。

然而，多个输入同时发生转换也会导致毛刺。这些毛刺无法通过添加硬件来修复。由于绝大多数“有趣的”系统在多个输入上同时(或接近同时)发生转换，”因此在大多数电路中，毛刺是’生活’中的一部分”。虽然我们已经展示了如何消除一种类型的毛刺，但讨论毛刺的重点不是为了消除它们，而是意识到它们的存在。在查看模拟器或示波器上的时序图时，这一点尤为重要。

Summary

数字电路是一个带离散电压值输入和输出的模块。它的规范描述了模块实现的功能和时序。这一章我们将重点放在组合电路上，其输出仅仅取决于当前的输入量。

下一章将介绍时序电路，它的输出取决于先前的输入和当前的输入。换句话说，时序电路对过去的状态有记忆能力。