Sequential Logic Design

在上一篇笔记中，我们展示了如何去分析和设计组合逻辑点。组合逻辑电路的输出只取决于电路的输入值。

Introduction

本篇笔记，我们会分析和设计时序逻辑(sequential logic)。时序逻辑的输出取决于当前和上一个状态的输入值，因此，时序逻辑具有记忆性。时序逻辑可能明确地记录下上一个输入的准确值，或许将先前的输入值提炼成一个更小的信息量，其被称为系统的状态(state)。数字时序电路的状态是一组被称为状态变量(state variables)的比特，其包含了过去的所有信息，这些信息是解释电路未来行为所必须的。

Latches and Flip-Flops

内存的最基本的构建块是双稳态(bistable)元件，一个有两个稳定状态的元件。下图(a)表示了一个简单的由一对逆变器连接在一个回路中组成的双稳态，下图(b)表示了相同的重绘的电路以强调对称性。逆变器之间是交叉耦合(cross-coupled)的，即$I1$的输入应为$I2$的输出，反之亦然。该电路没有没有输入，但有两个输出$Q$和$\overline {Q}$。

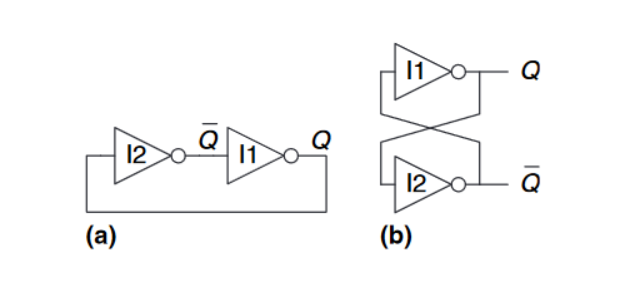
Cross-couple inverter pair

分析该电路不同于分析组合逻辑电路，因为它是循环的：$Q$依赖于$\overline {Q}$，而$\overline {Q}$依赖于$Q$。

考虑$Q$分别为0和1这两种情况：

  • 当$Q = 0$时：
    • 如下图(a)所示，$I2$接收一个$FALSE$输入$Q$，因此产生一个$TRUE$的输出$\overline {Q}$。于是$I1$接收一个$TRUE$的输入$\overline {Q}$，因此产生出一个$FALSE$的输出$Q$。这与原假设的$Q = 0$时一致的，因此称这种情况时稳定的
  • 当$Q = 1$时
    • 如下图(b)所示，同理，最终会得到一个为$TRUE$的输出$Q$，因此也是稳定的

因为交叉耦合的逆变器由两个稳定状态，因此这个电路被称为双稳态。不过，有一个微妙的观点是，电路有第三个可能的状态，两个输出大约在0和1之间，这被称为亚稳态(metastable state)，这将会在后续被讨论。

Bistable operation of cross-couple

一个$N$个稳定状态的元件可以传递$\log_2N \ bits$的信息，因此一个双稳态存储一个比特。交叉耦合逆变器的状态包含在一个二进制状态变量$Q$中，因此，$Q$的值告诉我们过去的一切，这对解释电路的未来行为是必要的。这个电路确实有另一个节点$\overline {Q}$，但是$\overline {Q}$不会包含任何额外信息，因为$Q$如果是确认的，那么$\overline {Q}$也一定随之确认。另一方面，$\overline {Q}$也是双稳态的一个可以接受的选项。

当电源首次作用于时序电路时，其初始状态是未知的，通常是不可预测的。并且每次电路导通时的状态也可能不同。

尽管交叉耦合逆变器能够存储一个信息比特，但是其并不实用，因为用户没有控制状态的输入。而锁存器(latches)和触发器(flip-flops)提供了控制状态变量的输入，因为我们考虑这两个双稳态元件。

SR Latch

最简单的时序电路是SR锁存器(SR Latch)，由两个交叉耦合的或非门组成。如下图所示，锁存器由两个输入$S$和$R$以及两个输出$Q$和$\overline{Q}$。$SR$锁存器类似于交叉耦合逆变器，但其状态可以通过$S$和$R$输入来控制，$S$和$R$输入对输出$Q$进行设置(set)和复位(reset)。

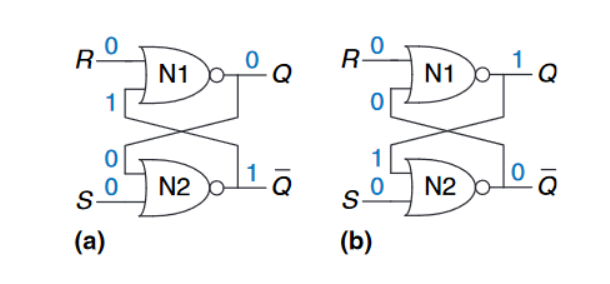
理解一个不熟悉的电路的作用就是写出它的真值表。回忆一下，当或非门的任意一个输入为$TRUE$，产生出一个输出$FALSE$：

  • 当$R = 1, S = 0$时：
    • $N1$首先看见至少一个输出$R$为$TRUE$，因此其产生一个为$FALSE$的输出$Q$。$N2$发现$Q$和$S$都是$FALSE$，因此产出一个$TRUE$的输出$\overline {Q}$
  • 当$R = 0, S = 1$时：
    • $N1$接受输入0和$\overline {Q}$。因为我们不再了解$\overline {Q}$，我们不能决定输出$\overline {Q}$。$N2$接收到至少一个为$TRUE$的输入$S$，因此其产生一个为$FALSE$的输出$\overline {Q}$。现在我们重新回顾$N1$，其两个输出都是$FALSE$，因此其输出$Q$为$TRUE$
  • 当$R = 1, S = 1$时：
    • $N1$和$N2$都能至少看见一个为$TRUE$的输入($R$或$S$)，所以其分别产出一个为$FALSE$的输出。因此$Q$和$\overline {Q}$都是$FALSE$
  • 当$R = 0, S = 0$时：
    • $N1$接受输入0和$\overline {Q}$。因为我们还不知道$\overline {Q}$，所以目前无法决定其输出。$N2$接受输入0和$Q$，因为我们不知道$Q$，因此也无法决定其输出。现在我们就被困住了，但我们直到$Q$要么是1，要么是0。因此我们可以检查每个子例来解决：
      • 当$Q = 0$时：
        • 因为$S$和$Q$都是$FALSE$的，所以$N2$产生一个为$TRUE$的输出$\overline {Q}$。现在$N1$就接收一个为$TRUE$的输入$\overline {Q}$，因此产出一个为$FALSE$的$Q$。正如我们所假设的那样
      • 当$Q = 1$时：
        • 因为$Q$是$TRUE$，因此$N2$产出一个为$FALSE$的输出$\overline{Q}$。现在$N1$接收两个$FALSE$的输入$R$和$\overline {Q}$，因此产生一个为$TRUE$的输出$Q$。正如我们所假设的那种

综上，在进入第四个情况之前，$Q$已经有了已知的先前值，被称为$Q_{prev}$。$Q_{prev}$是0或1，用于表示系统的状态。当$R$和$S$是0时，$Q$就会记住旧的值$Q_{prev}$，而$\overline {Q}$就是其补值$\overline {Q_{prev}}$。因此这个电路具有记忆性。

Bistable state of SR latch

下图中的真值表总结了上述的四种情况。输入$S$和$R$分别表示$Set$和$Reset$。设置一个比特意味着使它变为$TRUE$，重置一个比特意味着使其为$FALSE$。当$R$导通时，$Q$被重置为0而$\overline {Q}$与其相反。当$S$被导通时，$Q$被设置为1而$\overline {Q}$与其相反。当两个输出都没有被导通时，$Q$则会记录旧值$O_{prev}$。同时导通$S$和$R$时没有意义的，因为这就意味着锁存器需要同时设置和充值，这是不可能的。

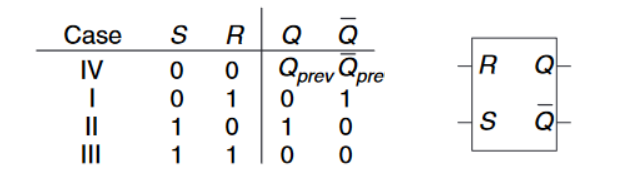
SR latch truth table and symbol

$SR$锁存器以上图中的右图的符号代替。和交叉耦合逆变器一样，$SR$锁存器是一个双稳态元件，一个比特的状态能够存储在$Q$中。无论过去发生了怎样的设置和重置，预测$SR$锁存器的未来行为所需要的仅仅只是最近一次设置或重置。

D Latch

$SR$锁存器是比较尴尬的，因为其在$S$和$R$都被导通时的行为是奇怪的。此外，输入$S$和$R$混淆了何时以及何物的问题。置位其中一个输出不仅确定了状态应该是什么，还确定了状态何时应该变化。当将这些因素分离开时，电路设计就会变得更加容易。下图显示的D锁存器(D latch)解决了这个问题。其有两个输入，数据(data)输入$D$控制下一个状态应该是什么和时钟(clock)输入$CLK$控制状态何时变化。

我们再一次分析该锁存器的真值表。为了方便起见，我们首先考虑内部节点$\overline {D}$、$S$和$R$。

  • 如果$CLK= 0$，$S$和$R$的值都为$FALSE$，则忽视$D$的值
  • 如果$CLK = 1$，那么一个与门将产生$TRUE$，另一个则是$FALSE$，这取决于$D$的值。
  • 在$S$、$R$、$Q$和$\overline {Q}$都如同$SR$锁存器一样被确定时：
    • 当$CLK = 0$时，$Q$会记录其旧值$Q_{prev}$
    • 当$CLK = 1$时，$Q = D$

因此，$D$锁存器避免了同时导通$S$和$R$的特殊情况。将所有内容整合在一起，我们看到时钟控制数据何时流过锁存器。当$CLK = 1$时，锁存器是透明(transparent)的。$D$处的数据会像锁存器只是一个缓冲器一样流过到$Q$。当$CLK = 0$时，锁存器是不透明的。它阻止新数据流过到$Q$，而$Q$保留旧值。因此，$D$锁存器有时被称为透明锁存器(transparent latch)或电平敏感锁存器(level-sensitive latch)。$D$锁存器的符号如图(c)所示。

D latch

当$CLK = 1$时，$D$锁存器连续更新其状态。我们将在本章后面看到，仅在特定时间点更新状态是很有用的。下一节描述的$D$触发器就是这样做的。

D Flip-Flop

D触发器(D Flip-Flop)可以由两个互补的时钟信号$CLK$控制的$D$锁存器背靠背地组成，如下图所示。其中，第一个锁存器被称为$master$，第二个锁存器被称为$slave$。$D$触发器的符号如图(b)所示，如果输出$\overline{Q}$不是必须的，可以用图(c)表示。

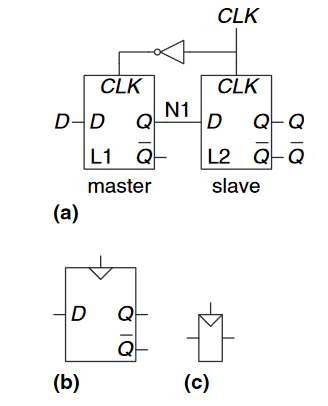
D Flip-flop

当$CLK = 0$时，$master$锁存器是透明的(数据流通的)，而$slave$锁存器是不透明的(数据不流通的)。因此，无论此时$D$是什么值都会传输到$N1$。当$CLK = 1$时，主锁存器变成不透明时，从锁存器变为透明的。在$N1$的值就可以传输到$Q$，但是$N1$被$D$截断。因此，在时钟从0跃迁到1之前，处于$D$的任何立即值都可以在时钟上升后复制到$Q$处。在其余的时刻，$Q$保存旧值，因为无论何时$D$和$Q$的路径之间都有一个不透明的锁存器块。

换句话说，$D$触发器在时钟上升沿时复制$D$到$Q$，并在其他时刻记住它的状态。为了简洁起见，时钟的上升沿通常被称为时钟边沿(clock edge)。输入$D$指定新状态将是什么，时钟边沿表示何时需要更新状态。

$D$触发器又被称为主从触发器(master-slave flip-flop)、边沿触发器(edge-triggered flip-flop)或正边沿触发器(positive edge-triggered flip-flop)。符号中的三角形表示边沿触发的时钟输入。在不需要输出$\overline{Q}$的情况下，其经常被忽略。

Register

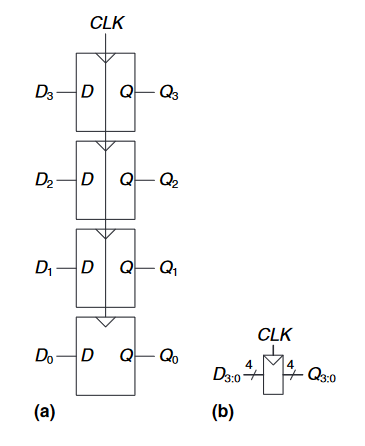
一个$N-bit$寄存器是由$N$个触发器组成的触发器组，其共享一个公共的$CLK$输入，使得寄存器的所有位同时被更新和保存。寄存器是绝大多数时序电路模块构成的关键，下图展示了一个四位寄存器的示意图和符号，输入$D_{3:0}$和输出$Q_{3:0}$都是四位总线的。

a 4-bit register

Enabled Flip-Flop

使能触发器(enabled flip-flop)添加另一个被称为$EN$或$ENABLE$的输出，以确定数据是否在时钟边沿时加载。当$EN$为$TRUE$时，使能触发器的行为就如同一个正常的$D$触发器；当$EN$是$FALSE$时，使能触发器忽略时钟输入并保存其原有状态。使能触发器在我们希望只在某些时刻加载一个新值，而非每一个边沿触发时是极其有用的。

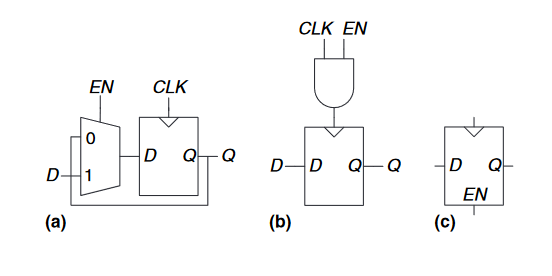
Enabled Flip-Flop

上图显示了两种构建使能触发器的方法。图(a)中的多路复用器选择了输入是否能够传递到$D$；图(b)中的时钟是一个与门，只有同时为真时才会使得触发器更新状态。注意，当$CLK = 1$时，$EN$不允许被改变，以免触发器看到时钟毛刺。因此，在时钟上执行逻辑是一个不好的行为。时钟门会延迟时钟，并可能导致时序错误。使能触发器的符号由图(c)所示。

Resettable Flip-Flop

可重置触发器(resettable flip-flop)添加了另一个被称为$RESET$的输入。当$RESET$是$FALSE$时，可重置触发器的行为和普通$D$触发器一样。当$RESET$是$TRUE$时，可重置触发器忽略$D$并重置输出为0。可重置触发器在我们第一次打开系统时，想把一个已知的状态强加到系统中的所有触发器时是很有用的。

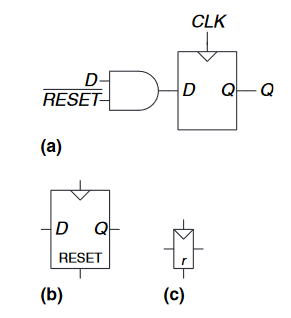
Resettable flip-flop

这种触发器可以同步(synchronously)或异步(asynchronously)复位。同步可重置触发器仅在$CLK$上升沿复位，而异步可重置触发器在$RESET$跃迁至$TRUE$时立即复位，与$CLK$无关。

上图中图(a)展示了如何从一个普通的$D$触发器和与门构建一个同步可重置触发器。当$\overline {RESET}$是$FALSE$时，与门就会强制输入一个0作为触发器的输入。当$\overline {RESET}$为$TRUE$时，与门就能传递$D$作为输入。因此，图(a)的$\overline {RESET}$表示其是一个低激活(active low)信号，而增加一个逆变器后，图(b)和图(c)展示了一个高激活(active high)信号的可重置触发器符号。

Putting It All Together

锁存器和触发器是构建时序电路的基本构建块。请记住，$D$锁存器是电平敏感的，而$D$触发器是边沿触发的。当$CLK = 1$时，$D$锁存器时透明的，允许$D$输入的数据流向输出$Q$。$D$触发器在$CLK$的上升沿时复制$D$的数据到$输出Q$。在其他时刻，锁存器和触发器都保持其状态。寄存器是一组多个$D$触发器构建的，其共用一个$CLK$信号。

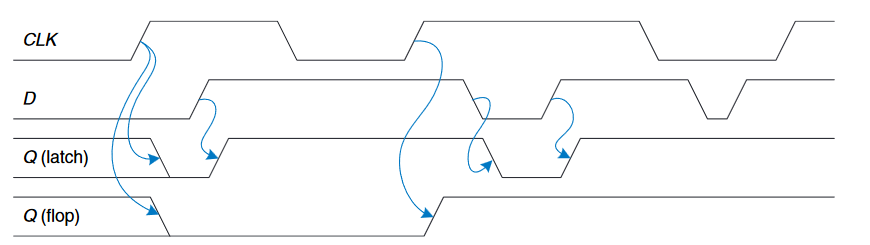
comparison waveforms

上图展示了锁存器和触发器的时序图，假设$Q$响应输入变化的延迟很小。箭头表示输出变化的原因。$Q$的初始值是为止的，可以是0或1，正如上图中的一组平行线所示。

  • 首先考虑锁存器，在$CLK$的第一个上升沿，$D = 0$，因此$Q$也必然变为0。每次改变$Q$，$Q$也随之变化。当$D$变化而$CLK = 0$时，忽略不计。
  • 现在考虑触发器，在$CLK$的每一个上升沿上，$D$被复制到$Q$上，其余时刻，$Q$保持其状态。

Synchronous Logic Design

一般来说，时序电路包含所有的非组合电路，也就是说，输出不能简单地通过查看当前输入来确定的电路。本节会介绍同步时序电路的概念和动态规约。

Some Problematic Circuits

多谐振荡器(astable circuits)
现在我们有三个被误用的逆变器形成的一个回路。如下图所示，第三个逆变器的输出被反馈到第一个逆变器的输入。每个逆变器的传播延时为$1ns$，请确定一下该电路的作用是什么？

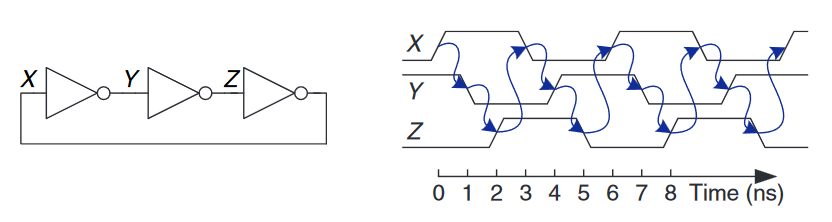
ring oscillator waveforms

假设$X$节点的初始值是0，那么$Y = 1, Z = 0$，从而又得出$X = 1$，因此与我们的原假设不符。这个电路没有稳定的状态，因此被称为不稳定的(unstable or astable)。上图表示了这个电路的行为。

如果$X$在0时刻上升，$Y$就会在$1ns$时下降，而$Z$就会在$2ns$时上升，$X$会在$3ns$时下降。下一轮时，$Y$在$4ns$时上升，$Z$在$5ns$时下降…然后持续重复。每个节点在$0 \thicksim 1$之间震荡，周期(也就是重复时间)为$6ns$。这种电路被称为环形振荡器(ring oscillator)。

环形振荡器的周期取决于每个逆变器的传播延时，而延时又取决于逆变器是如何制造的、电源电压甚至温度。因此，环形振荡器的周期很难确定。总之，环形振荡器是一个具有零输入和一个周期变化的输出的时序电路。

竞争条件(race condiyions)
这里我们设计了一个新的$D$锁存器，并宣称其比我们之前所介绍的锁存器更好，因为使用了更少的门。如下图所示。
请判断该锁存器是否工作正确？并且每个门是否独立延迟？

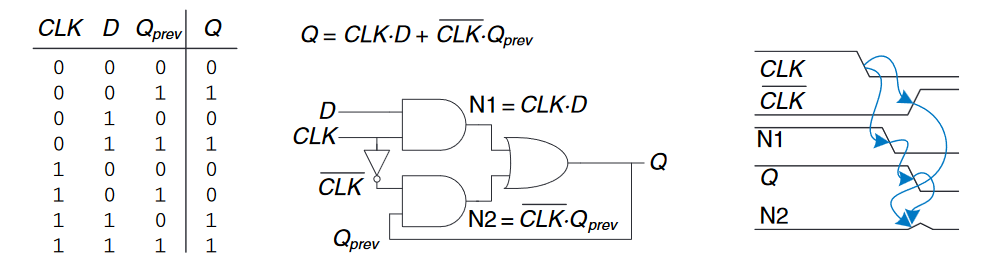
an improved? D latch

上图展示了该电路在某些门的速度比其他门慢时，会存在竞争条件使其失败。假设$CLK = D = 1$时，该锁存器是透明的，并且传递$D$使得$Q = 1$。那么现在$CLK$下降，锁存器应该记住旧值$Q_{prev}$使得保持$Q = 1$。然而，假设通过逆变器从$CLK$到$\overline {CLK}$的延迟相对于与门和非门的延迟要长，此时，节点$N1$和$Q$在$CLK$上升之前都可能下降。在这种情况下，$N2$永远都不会上升，从而使得维持$Q = 0$这一状况。

这是一个异步电路设计的例子，其中输出直接反馈到输入。异步电路因存在竞争条件而臭名昭著，电路的行为取决于逻辑门中哪条路径是最快的。一个电路可能工作正常，而另一个看似相同但由具有稍有不同延迟的门构建的电路可能不工作。或者该电路可能仅在某些温度或电压下工作，而这些温度或电压下的延迟恰到好处。这些故障极其难以追踪。

Synchronous Sequential Circuits

上面的两个例子包含循环路径，其中输出直接反馈到输入。如果将一个输入应用到组合电路中，则在一个传播延时内，输出总会收敛到正确的值。然而，具有循环路径的时序电路可能存在不期望的竞争或不稳定的行为。

为了避免这种情况，通常使用在路径的某处插入寄存器来打断循环路径。这就将电路转化为一个组合逻辑和寄存器的集合。寄存器包含该系统的状态，并且只在边沿触发时改变，因此我们称其该状态与时钟同步(synchronized)。如果时钟速度足够慢，使得在下一个时钟边沿到来之前所有的寄存器的输入都已经稳定，那么所有的竞争条件便被消除。在循环路径中使用寄存器的这种规约，我们就得出了同步时序电路的正式定义。

时序电路有一个有限的离散状态集合$S_0, S_1, \cdots, S_{k - 1}$。同步时序电路有一个时钟输入，其上升沿指示状态转变发生的时间序列。我们通常使用输入当前状态和下一个状态来区分系统当前的状态和其将要进入的下一个时钟边沿的状态。时序电路的功能准则详细说明了对于每种可能的当前状态和输入值的组合的下一个状态和每一个输出的值。而时序规范包括时钟上升沿到输出变化的时间上界$t_{pcq}$和下界$t_{ccq}$，以及相对于时钟上升沿时输入必须稳定的设置和保持时间$t_{setup}$和$t_{hold}$。

同步时序电路的构成规则告诉我们，如果一个电路是由相互连接的元件构成的，则称其为同步时序电路。

  • 每个电路元件要么是寄存器，要么是组合电路
  • 至少一个电路元件是寄存器
  • 所有的寄存器接收相同的时钟信号
  • 每一个循环路径包含至少一个寄存器

不同步的时序电路被称为异步时序电路。

触发器是一个最简单的同步时序电路。其有一个输入$D$，时钟$CLK$，输出$Q$和两个状态${0, 1}$。触发器的功能规范是下一个状态是$D$，而$Q$是当前状态。另外两个最常见的同步时序电路被称为有限状态机和流水线，这将在后续介绍。

判断哪一个是同步时序电路

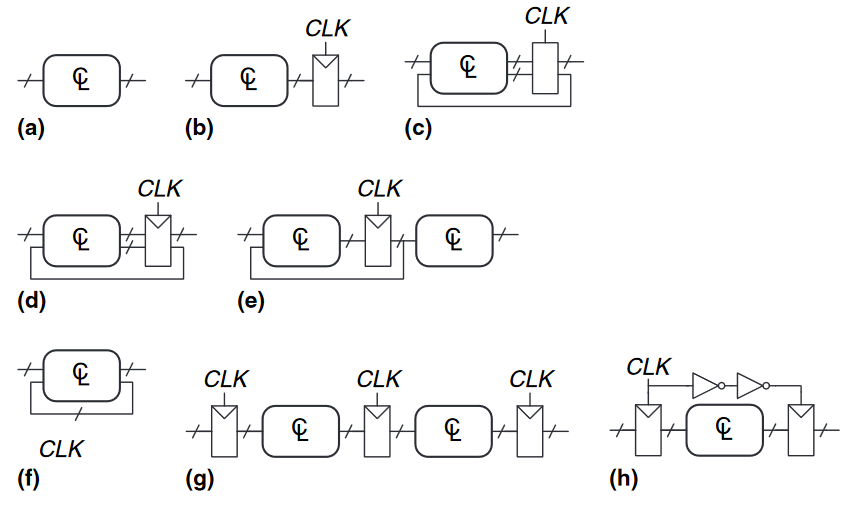
example circuits

  • 图(a)是组合电路而非时序电路
  • 图(b)是一个无反馈的简单时序电路，但不同步
  • 图(c)既不是组合电路也不是同步时序电路，因为其有一个既不是组合电路又不是寄存器的锁存器元件
  • 图(d)、图(e)是同步时序电路，同时也是简单的有限状态机
  • 图(f)既不是组合电路也不是同步时序电路，因为在回路上没有寄存器
  • 图(g)是同步时序电路，也是流水线形式
  • 图(h)不是严格意义上的同步时序电路，因为第二个寄存器接收了一个不同的时钟信号(其延迟由两个逆变器决定)

Synchronous and Asynchronous Circuits

异步设计在理论上比同步设计更具有一般性，因为系统的时序不受时钟寄存器的限制。就如同模拟电路比数字电路更具一般性。但是，同步电路已经被证明比异步电路更容易设计和使用，并且尽管对一部电路进行了数十年的研究，但几乎所有的数字系统本质上都是同步的。

当然，异步电路在具有不同时钟的系统之间通信或者任意时间接收输入时偶尔是有必要的。

Finite State Machine

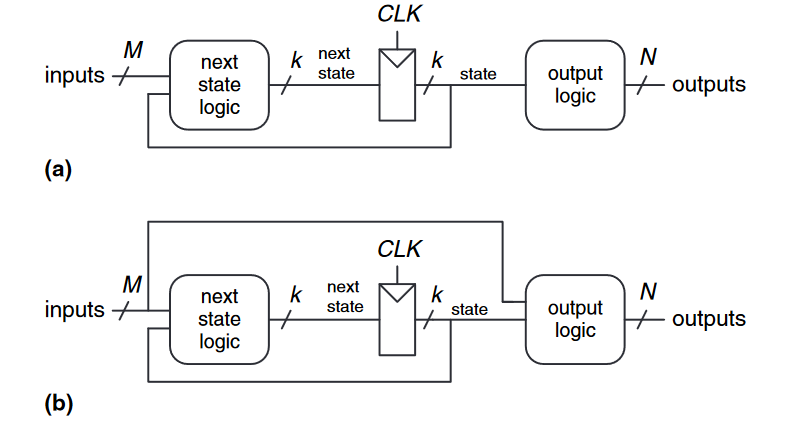
同步时序电路可以以一种叫做有限状态机(finite state machine, FSM)的形式画出，如下图所示。其之所以被叫做有限状态机，是因为一个带有$k$个寄存器的电路可以处于有限数量$2^k$个唯一状态中的一个状态。一个有限状态机有$M$个输入，$N$个输出以及$k$比特状态。其也接收一个时钟和重置(可选)信号。一个有限状态机由两个组合逻辑组成，即下一个状态逻辑和输出逻辑，以及一个存储状态的寄存器。在每个时钟边沿上，有限状态机就会进入下一个状态，该状态是由当前状态和输入计算出来的。有两种常见的状态机类别，它们根据自身的功能准则来区分。

  • $Moore Machines$
    • 输出只取决于机器的当前状态
  • $Mealy Machines$
    • 输出取决于机器的当前状态以及当前输入

在给定功能准则的前提下，有限状态机提供了一种系统化的方法来设计同步时序电路。

Finite state machines

FSM Design Example

为了解释有限状态机的设计，考虑在校园繁忙的路口发明一个交通控制灯的问题。

我们决定使用有限状态机来实现这个问题，我们在十字交叉的两个道路上分别安装两个交通传感器$T_A$和$T_B$。如果检测到学生，那么每个传感器都表示为$TRUE$；反之则为$FALSE$。同时，再安装两个交通灯$L_A$和$L_B$来控制交通。每个灯接收数字输入来指定红黄绿三色。因此，我们的有限状态机有两个输入$T_A$和$T_B$，两个输出$L_A$和$L_B$。同时，我们还提供了一个周期为$5s$的时钟和复位按钮以置于已知的初始状态。如下图所示。

fsm machines

下一步我们就画出如上图所示的状态机草图，表示了系统中所有可能的状态以及这些状态之间的转变。当系统被重置时，$L_A$就应该时绿灯而$L_B$就是红灯。每五秒钟，控制器就会检查交通模式并决定下一步要做什么。一旦$Academic Ave$上有车流，那么这个信号灯就不应该被改变。当不再有车流时，那么就应该在其变黄五秒后变为红灯；而$Bravado Ave$的灯光就变成绿灯。类似的，如果$Bravado$上有车流，那么持续绿灯，如果没有，则就变为黄灯再变为红灯。

在一个状态转移图中，圆圈表示状态，圆弧表示状态之间的转变。状态转换发生在时钟的上升沿。此外，时钟只简单的控制状态该何时发生，而状态图表示哪些转变发生。标记为$Reset$的圆弧从外部空间指向$S_0$，表示系统在复位时应进入该状态，不论其先前的状态是什么。如果一个状态有多个圆弧离开，需要在每个弧上标记每个转换是由哪个输入触发的。如果一个状态只有一个弧离开，且该弧为标记，就说明无论输入如何，该状态总是会转变到所指向的状态。

我们将状态转移图重写为状态转移表，表示对于每个状态和输入。下一个状态$S’$应该是什么。注意，当下一个状态不依赖于某个特定输入时，表中使用$Don’t Cares$符号$X$来表示。同时也应该注意，外来符号$Reset$应该省略。

状态转移图是抽象的，其使用标记为${S_0, S_1, S_2, S_3}$的状态和标记为${red, yellow, green}$的输出。要建立一个实际的电路，必须对状态和输出进行二进制编码。下图是对其编码的展示，每个状态和输出用两个比特编码：$S_{1:0}$，$L_{A1:0}$和$L_{B1:0}$

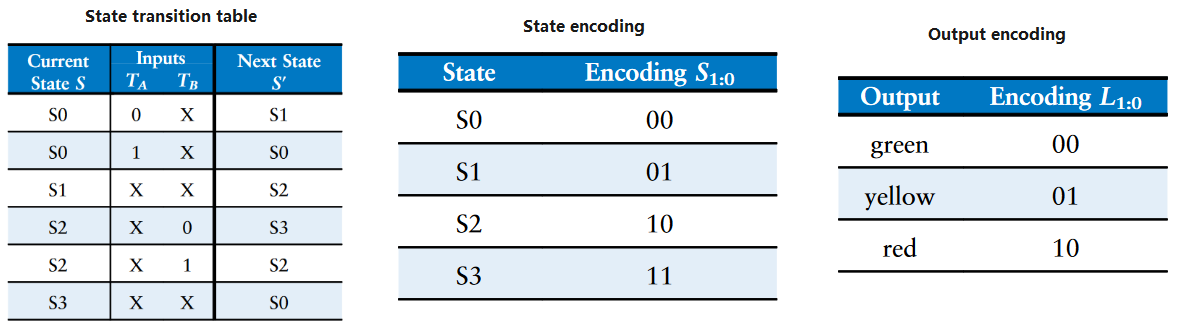
state tables

然后我们使用得出的编码更新状态转移表，如下图所示。修改后的状态转移表就是一个真值表，其规定了下一个状态的逻辑。它将下一个状态$S’$定义为当前状态$S$和输入的函数。

state transition table

从这个真值表中，以乘积和规范式读出下一个状态的布尔方程是很简单的：

$$
S_1’ = \overline {S_1}S_0 + S_1\overline {S_0}\overline {T_B} + S_1\overline {S_0}T_B
$$

$$
S_0’ = \overline {S_1}\overline {S_0}\overline {T_A} + S_1\overline {S_0}\overline {T_B}
$$

上述等式可以通过卡诺图简化，但是这里我们直接观察可以看出：\overline {T_B}和$T_B$是可以简化的，并且$S_1’$可以被归结为异或运算。因此：

$$
S_1’ = S_1 \oplus S_2
$$

$$
S_0’ = \overline {S_1}\overline {S_0}\overline {T_A} + S_1\overline {S_0}\overline {T_B}
$$

和上述一样，我们以相同的方式写出一个输出的真值表，表明对于每个状态，该状态下的输出应该是什么。然后得出其布尔方程。

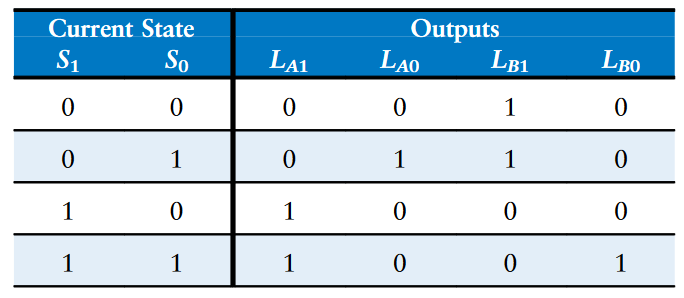
output table

$$
L_{A1} = S_1 \qquad L_{A0} = \overline {S_1}S_0
$$

$$
L_{B1} = \overline {S_1} \qquad L_{B0} = S_1S_0
$$

最终，我们可以画出一个$Moore$状态机。

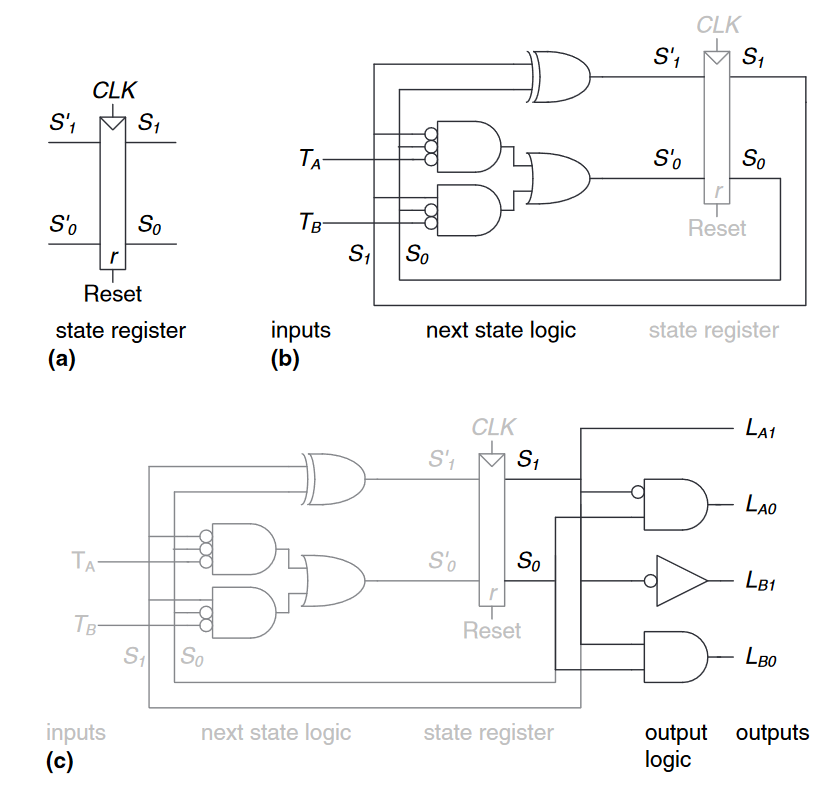
首先，我们先画出一个$2-bit$状态寄存器，如下图(a)所示。在每个时钟边上，状态寄存器复制下一个状态$S_{1:0}’$成为$S_{1:0}$。状态寄存器启动时接收同步或异或重置以初始化状态机。

然后，我们根据得出的$S_1’$和$S_0’$的布尔方程绘制状态逻辑，该逻辑从当前状态和输入中计算下一个状态，如图(b)所示。

最后，我们根据得出的输出布尔方程绘制输出逻辑，该逻辑从当前状态计算输出，如图(c)所示。

state machine circuit

下图展示了交通灯控制器经过状态序列的时序图。该图显示了$CLK$、$Reset$，输入$T_A$和$T_B$，下一个状态$S’$，当前状态$S$以及输出$L_A$和$L_B$。箭头表示因果关系，虚线表示状态变化时的时钟上升沿。

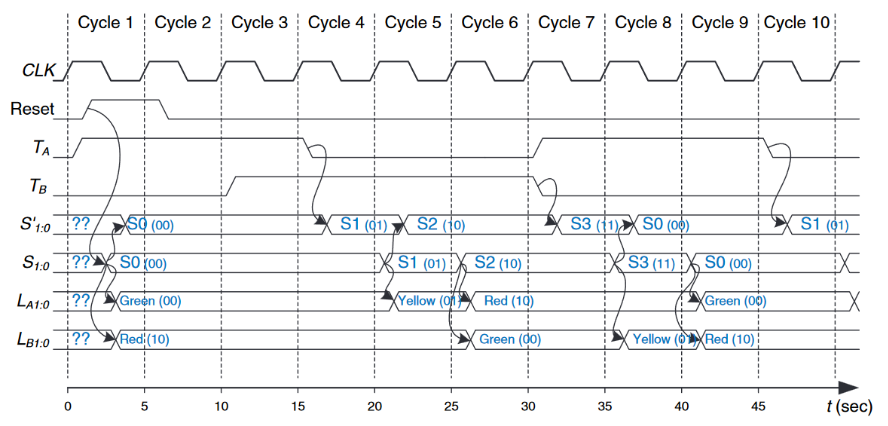
timing diagram for traffic

该时钟具有$5s$一个周期，因此交通灯最多$5s$换一次。当有限状态机首次开启时，其状态是未知的，因此需要对系统进行重置进入已知状态。在该时序图中，$S$会立即重置为$S_0$，表示正在使用异步可复位的触发器。在状态$S_0$中，$L_A$是绿色而$L_B$是红色。

State Encodings

在上一个例子中，输出和状态的编码是任意选择的。不同的选择会导致不同的电路。一个很自然的问题是：如何确定产生逻辑门最少或传播延迟最短的电路的编码？不幸的是，找到最佳编码没有简单的方法，除了尝试所有可能性，当状态数量很大时，这是不可行的。然而，通常可以通过观察来选择一个好的编码，以便相关的状态或输出共享位。计算机辅助设计($CDA$)工具也擅长搜索可能的编码集并选择一个合理的编码。

状态编码中的一个重要决策是在二进制编码和独热(复习：独热指的是一次只有一个输出为$TRUE$)编码之间进行选择。

  • 使用二进制编码，就像在交通灯控制器示例中使用的那样，每个状态都表示为一个二进制数。因为$K$个二进制数可以用$log_2K$位表示，所以具有$K$个状态的系统只需要$log_2K$位的状态。
  • 在独热编码中，每个状态都使用一个单独的状态位。它被称为one-hot，因为任何时候只有一个状态位是hot或$TRUE$。例如，一个具有三个状态的独热编码的$FSM$将具有状态编码$001$、$010$和$100$。每个状态位都存储在一个触发器中，因此独热编码需要比二进制编码更多的触发器。然而，使用独热编码时，下一个状态和输出逻辑通常更简单，因此需要更少的门。

因此，最佳编码的选择得根据具体的有限状态机来进行分析。

Moore and Mealy Machines

至今为止，我们已经展示了$Moore Machine$的例子，其输出仅依赖于系统的状态。因此在$Moore Machine$的状态转移图中，输出被标注在圆圈中。$Mealy Machine$和$Moore Machine$很相似，不过其输出同时取决于系统状态和输入。因此，$Mealy$的状态转移图中的输出被标记在圆弧上，而非圆圈中。

Moore Versus Mealy Machines
我们拥有一只带有$FSM$大脑的宠物机器蜗牛。这只蜗牛沿着一个包含一系列1和0的纸带从左到右爬行。在每个时钟周期，蜗牛爬到下一个位。当蜗牛爬过的最后两个位是从左到右为01时，蜗牛会微笑。设计$FSM$来计算蜗牛何时应该微笑。输入$A$是蜗牛触角下方的位。当蜗牛微笑时，输出$Y$为$TRUE$。比较$Moore$和$Mealy$状态机设计。为每个机器草拟一个时序图，显示蜗牛沿着序列·0100110111·爬行时的输入、状态和输出。

$Moore Machine$需要三个状态，如下图中图(a)所示；相比而言，$Mealy Machine$只需要两个状态。如图(b)所示，每个弧段标记为$A/Y$，其中$A$为引起该转变的输入值，$Y$是对应的输出。

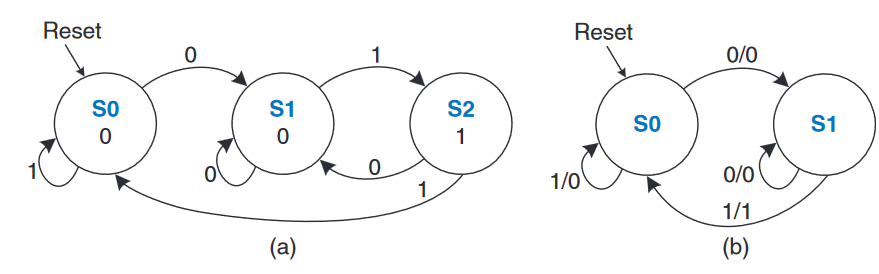
FSM state transition diagrams

下表展示了$Moore Machine$的状态转换表和输出表。$Moore$至少需要两个比特的状态。考虑采用二进制状态编码：$S_0 = 00, S_1 = 01, S_2 = 10$，下图表示了使用编码重写后的状态转换表和输出表。

Moore table

从这些表中，我们可以发现下一个状态和输出的布尔方程：

$$
S_1’ = S_0A \qquad S_0’ = \overline {A}
$$

$$
Y = S_1
$$

下面则表示了$Mealy$的状态转换表和输出表。$Mealy$只需要一个比特的状态。考虑采用二进制编码：$S_0 = 0, S_1 = 1$。下图也以二进制编码重写了输出表和状态转换表。

Mealy table

从上述的表中，我们可以得出其下一个状态和输出的布尔方程：

$$
S_0’ = \overline {A}
$$

$$
Y = S_0A
$$

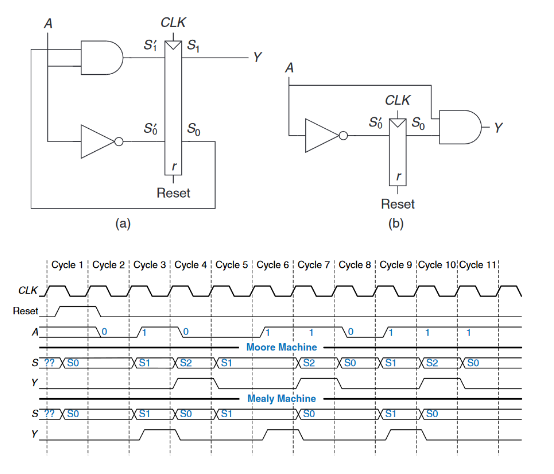
$Moore$和$Mealy$的电路图(图(a)是$Moore$，图(b)是$Mealy$)和时序图下图所示。这两台机器遵循不同的状态序列。此外，$Mealy$机的输出会比较早一个周期上升，因为它对输入做出响应，而不是等待状态改变。如果通过一个触发器延迟$Mealy$输出，它将与$Moore$输出匹配。在选择$FSM$设计风格时，请考虑你希望输出何时响应。

FSM schematics

Factoring State Machine

如果一个状态机能够被分解成多个相互作用的简单状态机使得一些机器的输出是另一些机器的输入，那么设计复杂的状态机通常是容易的。这种层次化和模块化的应用被称为状态机的分解(factoring of state machines)。

Unfactored and factored state machines
修改我们在之前做的交通灯控制器，使其拥有一个游行模式，该模式保持$Bravado$的灯当观众和乐队以分散的团体向足球比赛进军时一直是绿灯。控制器接收两个新的输入：$P$和$R$，如果$P$导通至少一个周期进入巡游模式；而$R$导通至少一个周期结束巡游模式。在游行模式下，控制器按照正常的顺序进行，直到$L_B$变绿，然后保持在该状态下，直到游行模式结束。
首先，我们给出一个有限状态机的草图，如下所示；然后，给出两个相互作用的有限状态机的状态转换图。$Mode$状态机在导通时输出$M$；$Lights$状态机基于$M$和$T_A$、$T_B$来控制灯。

state controller FSM

上图中图(a)的状态机图显示了单个状态机的设计。状态$S_0 \thicksim S_1$处理正常模式，状态$S_4 \thicksim S_7$处理游行模式。途中的这两部分几乎完全相同，但在游行模式下，状态机仍停留在$S_6$，因此$Bravado$上仍亮着绿灯。输入$P$和$R$控制这两部分的运动，状态机的设计较为凌乱繁琐。

而图(b)显示了两种类型的状态机，$Mode$状态机用于跟踪灯光是否处于正常或游行模式；当$M$为$TRUE$时，$Lights$状态机被修改为保持在$S_2$状态。

Deriving an FSM from a Schematic

从示意图中导出状态转移图几乎是遵循状态机设计的逆过程。当在逆向别人的工程或查看一个不完善的文档时，这个过程可以是必要的。

  • 检查电路，说明输入、输出和状态位
  • 写出下一个状态和输出的布尔等式
  • 创建出下一个状态和输出表
  • 缩减下一个状态表，消除不可达状态
  • 分配每一个有效状态位组合一个名字
  • 使用分配的状态名重写下一个状态和输出表
  • 画出状态转移图
  • 陈述状态机的每一步操作

最后一步，必须要小心简洁的描述状态机的整体目的和功能，不要简单地重述状态转换图的每一个转换。

Timing of Sequential Logic

我们回忆一下，触发器在时钟上升沿时将输入$D$复制到输出$Q$上，这种过程被称为采样(sampling)。如果$D$在时钟上升沿时稳定在0或1，则此行为的定义是明确的。那么，如果$D$在上升沿时发生了改变呢？

这个问题就类似于相机在抓拍一张图片时面临的问题。试想一下，拍摄一只青蛙从荷叶上跳入水中的情况。如果你在跳跃前拍摄，你会看到荷叶上有一只青蛙；在跳跃后拍摄，则会看到水中的涟漪；如果你在青蛙正在跳跃时拍摄，你可能会看到一张模糊的图像。相机的一个特点就是有一个光圈时间(aperture time)，在这个时间内，物体必须保持静止才能捕获到清晰的图像；同样，时序元件在时钟边缘附近也有一个光圈时间，在这个时间内，输入必须是稳定的才能使触发器产生良好定义的输出。

时序元件的光圈时间被时钟边缘前的建立时间(setup time)和其后的保持时间(hold time)所定义。就如同静态规约限制我们使用禁区之外的逻辑电平一样，动态规约限制我们使用在光圈时间外的发生变化的信号。通过利用动态规约，我们可以把时间看作是一个离散单位，称为时钟周期，就如同我们电平信号看作是离散的1和0一样。一个信号可能在一定时间内产生毛刺和大范围的振荡。在动态规约下，我们只关心在时钟周期结束时的最终值，即在信号到达一个稳定值时。因此，我们可以简单的写为$A[n]$，表示信号$A$在第$n$个时钟周期结束时的值，其中$n$是整数；而不是用$A(t)$表示，其表示$A$信号在某一时刻$t$的值，其中$t$是任意实数。

时钟周期必须足够长，使得所有的信号都能稳定。这就对系统的速度提出了限制，在实际系统中，时钟并不能精确的同时到达所有触发器。这种时间上的变化，称为时钟偏差(clock skew)，进一步增加了必须要的时钟周期。

有时满足动态规约是不可能的，特别是在与现实世界进行接口时。例如，考虑一个电路，其输入来自按钮。一只猴子可能会在时钟上升时按下按钮。这可能导致一种称为亚稳态(metastability)的现象，其中触发器捕获了介于0和1之间的值，需要花费无限长的时间才能解析为一个良好的逻辑值。对于这样的异步输入，解决方案是使用一个同步器，它有很小的(但非零)概率产生非法逻辑值。

The Dynamic Discipline

我们已经讨论了时序电路的功能准则，现在让我们来看一看时序电路的时许准则，如下图所示。

timing specification

当时钟上升沿时，输出可能在时钟到输出$Q$之间的污染延迟$t_{ccq}$之后开始变化，并且在传播延时$T_{pcq}$内确定到稳定状态的最终值，污染延迟和传播延迟分别代表电路中的最快和最慢延迟。为了使电路正确采样其输入，输入必须在时钟上升沿之前必须稳定在至少一段建立时间$t_{setup}$和在时钟上升沿之后的一段保持时间$t_{hold}$。建立时间和保持时间之和被称为电路的光圈时间，因为这是输入必须保持稳定的总时间。

动态规约指出，同步时序电路的输入必须在上升沿的光圈时间附近建立和保持一个稳定状态。这一要求使得触发器采样信号不会被改变，并且由于我们只关心输入在采样时刻的最终值，因此我们可以将信号在时间和逻辑上都视为离散的。

System Timing

时钟周期或周期时间$T_{c}$为重复时钟信号上升沿之间的时间，其倒数被称为时钟频率$f_c = 1/T_c$。其他条件不变的情况下，增加时钟频率会增加数字系统每单位时间可以完成的工作量，频率以赫兹$Hz$为单位进行测量，即每秒周期数：$1MHz = 10^6Hz$，$1GHz = 10^9Hz$。

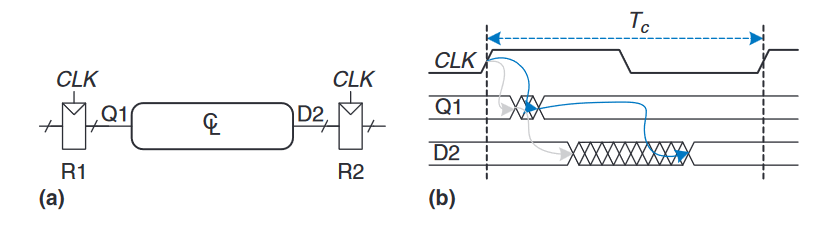
Path between registers and timing diagram

图(a)说明了一个同步时序电路中的一般路径，其时钟周期是我们想要计算的。在上升沿上，寄存器$R1$输出$Q1$，信号进入逻辑组合块中，输出$D2$，作为输入进入$R2$。该时序图由图(b)所示，每个输出信号在其输入发生变化后可能会在污染延迟后开始变化，并在其输入稳定后的传播延迟内稳定最终值。灰色箭头表示通过$R1$和组合逻辑的污染延迟，蓝色表示通过$R1$和组合逻辑的传播延迟。我们针对第二个寄存器$R2$的建立时间和保持时间进行时序约束分析。

Setup Time Constraint

下图仅表示通过路径的最大延迟，用蓝色箭头表示。为了满足$R2$的建立时间，$D2$必须不晚于下一个时钟周期之前的建立时间，因此，我们找到一个关于最小时钟周期的方程：

$$
T_c \ge t_{pcq} + t_{pd} + t_{setup}
$$

触发器时钟到输出$Q$的传播延时$T_{pcq}$和建立时间$t_{setup}$由制造商指定。因此我们将上述的方程重新排列，以逻辑组合求解最大传播延迟，而组合逻辑通常是个体设计者控制下的唯一变量。

$$
t_{pd} \le T_c - (t_{pcq} + t_{setup})
$$

上述中括号里面的项$t_{pcq} + t_{setup}$被称为时序开销(sequencing overhead)。理想情况下，整个周期时间$T_c$将可用于组合逻辑中的有用计算，即$T_{pd}$。然而，触发器的时序开销会占据这段时间。方程$t_{pd} \le T_c - (t_{pcq} + t_{setup})$被称为建立时间约束(setup time constrain)或最大延迟约束(max-delay constrain)，因为它取决于建立时间并限制了组合逻辑中的最大延迟。

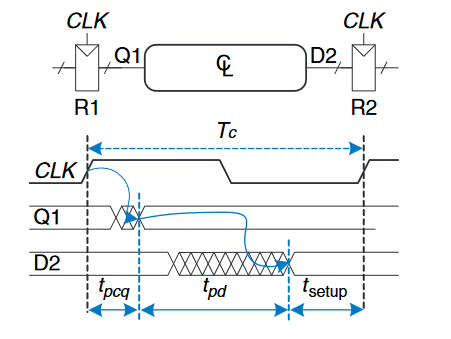
Maximum delay for setup time constraint

如果通过组合逻辑的传播延迟太大，那么$D2$就可能在$R2$需要稳定值采样时还没达到其最终值。因此，$R2$可能会采样到一个错误的结果，甚至是处于禁区的非法的逻辑层次。该问题可以通过增加时钟周期或重新设计组合逻辑以获得更短的传播时延来解决。

Hold Time Constraint

在上面的例子中，$R2$寄存器也有一个保持时间约束(hold time constraint)。输入$D2$不能被改变，直到时钟上升沿后的$t_{hold}$时间过后。如下图，$D2$可能在时钟上升沿后的$t_{ccq} + t_{cd}$后被改变。因此，

$$
t_{ccq} + t_{cd} \ge t_{hold}
$$

当然，$t_{ccq}$和$t_{hold}$同样也是触发器的特定，因此不再设计者的控制范围内。所以，我们需要对该式进行重排来求解最小污染延迟：

$$
t_{cd} \ge t_{hold} - t_{ccq}
$$

上式通常被称为保持时间约束或最小延迟约束(min-delay constraint)，因为其限制了通过组合逻辑的最小延迟。

我们假设任何逻辑元件之间都可以互相连接，而不引入时序问题。尤其是，我们希望两个触发器直接级联，而不会引起保持时间问题。在这个例子中，$t_{cd} = 0$，因为触发器之间没有逻辑组合，因此：

$$
t_{hold} \le t_{ccq}
$$

换句话说，可靠的触发器必须有一个比污染延迟短的保持延时。通常而言，触发器通常的设计为$t_{hold} = 0$，因此上式是始终成立的。除非另有说明，否则在笔记中中我们通常会做出这样的假设，并忽略保持时间约束。

然而，保持时间约束非常重要。如果违反了这些约束，唯一的解决方案是增加逻辑中的污染延迟，这需要重新设计电路。与建立时间约束不同，它们不能通过调整时钟周期来修复。在当今先进技术中，重新设计集成电路并制造修正设计需要数月时间和数百万美元的投资，因此必须非常严肃地对待保持时间违规行为。

Metastability

如先前所说，我们不能保证时序电路的输入在光圈时间内始终稳定，特别是当输入来自外部时。考虑一个按钮被连接到触发器的输入的情况，如下图所示。当按钮没有按下时，$D = 0$;反之，$D = 1$。一只猴子在相对于$CLK$上升沿的某个随机时间点按下按钮，我们想知道$CLK$上升沿之后的输出$Q$的值。

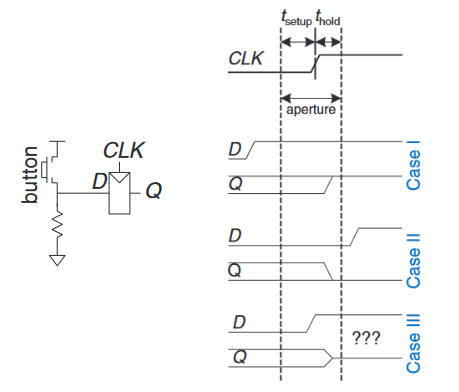
  • 例一，当按钮在$CLK$之前被按下时，输出$Q = 1$
  • 例二，当按钮在$CLK$之后被按下时，输出$Q = 0$
  • 例三，当按钮在$CLK$的建立时间$t_{setup}$后，保持时间$t_{hold}$前按下时，输出此时不能确定。

Metastable State

当触发器采样一个在其光圈时间内变化的输入时，输出$Q$可能会瞬间承受一个介于0和$V_{DD}$之间的电压，而这个电压处于禁区之内，这被称为亚稳态(metastable)。最终，触发器就会将输出解析为0或1的稳定状态。然而，达到稳定状态的解析时间是无界的。

如下图所示，触发器的亚稳态类似于两个山谷之间的山峰上的一个球。这两个山谷是稳定状态，因为球在山谷里不受干扰的情况下会保持在那里。山顶上的平衡点称为亚稳态，因为如果球完美平衡，它会保持在那里。但由于没有什么是完美的，球最终会朝一个方向或另一个方向滚动。这种变化所需的时间取决于球最初的平衡程度。每个双稳态设备在两个稳定状态之间都有一个亚稳态。

metastable

Resolution Time

如果一个触发器的输入在时钟周期内随机变化，那么解析到稳定状态所需的解析时间$t_{res}$也是一个随机变量。如果输出在光圈时间外变化，则$t_{res} = t_{pcq}$。一旦输出在光圈时间内变化，那么$t_{res}$就会大幅度变长。解析时间$t_{res}$超过某个任意时间$t$的概率随着$t$的增加呈指数下降：

$$
P(t_{res} \lt t) = \frac{T_0}{T_c}e^{-\frac{t}{\tau}}
$$

其中，$T_c$是时钟周期，$T_0$和$\tau$是触发器的特性。该方程仅对$t$长于$t_{pcq}$的情况有效。

直观地说，$T_0/T_c$描述了输入在不良时间(即在光圈时间内)发生变化的概率；这个概率随着周期时间$T_c$的增加而减少。$\tau$是一个时间常数，表示触发器从亚稳态移动出去的速度；它与触发器中交叉耦合门的延迟有关。

总之，如果一个双稳态设备如触发器的输入在光圈时间内发生变化，输出可能在解析为稳定的0或1之前持续处于亚稳态值。解析所需的时间是不受限制的，因为对于任何有限时间$t$，触发器仍然处于亚稳态的概率是非零的。然而，随着$t$的增加，这个概率指数级下降。因此，如果我们等待的时间足够长，远远超过$t_{pcq}$，我们可以极高的概率期待触发器达到有效的逻辑电平。

Synchronizers

现实中，对数字系统的异步输入是不可避免的。例如人类的输入是异步的，如果这些输入处理不当就会导致系统内的亚稳态电压，从而引起难以跟踪和纠正的不稳定的系统故障。数字系统的设计者的目标应该是确保给定异步输入时，遇到亚稳态的几率足够小。“足够”需要取决于环境，对于手机来说，十年一次故障也许是能接受的；对于一个医疗设备来说，在宇宙的预期寿命中发生一次故障或许是一个更好的目标。为了保证良好的逻辑水平，所有的异步输入都应该被同步地传入。

如下图所示的同步器(Synchronizers)，其可以接收一个异步输入$D$和时钟信号$CLK$。它在有限的时间内产生一个输出$Q$；并且该输出极高概率是一个有效的逻辑电平。如果$D$在光圈时间内是稳定的，输出$Q$就应该和$D$的值一样；如果$D$不稳定，$Q$就可能是$HIGH$或$LOW$，但不一定是亚稳态。

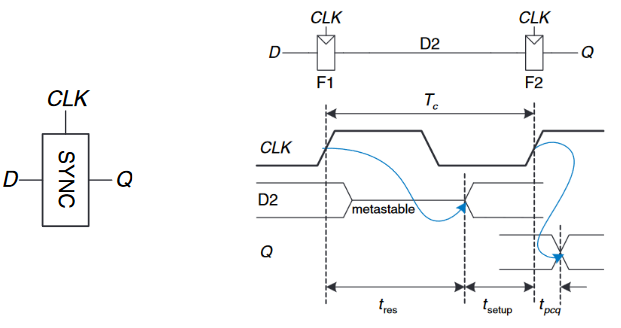
simple synchronizer

上图也给出了一个简单的方式来构建一个同步器：用两个触发器。$F1$在$CLK$上升沿处采样$D$，如果$D$正在改变，那么输出$D2$就可能暂时处于亚稳态；如果时钟周期足够长，$D2$就有很高的概率在时钟周期结束前收敛到一个有效的逻辑电平。然后$F2$采集稳定状态下的$D2$，产生出一个良好输出$Q$。

如果同步器的输出$Q$是亚稳态的，那么该同步器就是失效的。这发生在$F2$需要进入建立时间，$D2$还未被解析到一个有效值时，即如果$t_{res} \gt T_c - t_{setup}$时。通过之前我们得到的概率式($P(t_{res} \lt t) = \frac{T_0}{T_c}e^{-\frac{t}{\tau}}$)，单个输入在随机时刻失败的概率为：

$$
P(failure) = \frac{T_0}{T_c}e^{-\frac{T_c - t_{setup}}{\tau}}
$$

失败概率$P(failure)$是输出$Q$在单次$D$变化时处于亚稳态的概率。如果$D$每秒变化一次，每秒的失败概率就是$P(failure)$。但是，如果$D$每秒变化$N$次，则每秒发生故障的概率为$N$倍：

$$
P(failure) / sec = N\frac{T_0}{T_c}e^{-\frac{T_c - t_{setup}}{\tau}}
$$

系统的可靠性通常用平均故障时间间隔(mean time between failures, MTBF)来衡量。顾名思义，$MTBF$就是系统在任意给定秒内发生故障的概率的倒数：

$$
MTBF = \frac{1}{P(failure) / sec} = \frac{T_ce^{-\frac{T_c - t_{setup}}{\tau}}}{NT_0}
$$

上面的方程表明，随着同步器的等待时间$T_c$增加，$MBTF$呈指数增加。对于绝大多数系统，等待一个时钟周期的同步器提供了一个安全的$MTBF$，在高速系统中，可能需要等待更多的周期。

Parallelism

系统的速度由信息在其中移动的延迟和吞吐量来表征。我们将令牌(token)定义为一组输入，经过处理后产生一组输出。系统的延迟是一个令牌从开始到结束通过系统所需的时间，吞吐量是单位时间内可以产生的令牌数量。

可以想象，通过同时处理多个令牌可以提高吞吐量。这被称为并行(parallelism)，其有两种形式：空间的和时间的。利用空间并行性(spatial parallelism)，提供多个硬件副本从而在同一时刻完成多个任务；利用时间并行性(temporal parallelism)，任务被分成多个阶段，就像一条分配线。多任务可以跨阶段展开执行。尽管每个任务都需要经过所有阶段，但每个阶段的任意时刻都会有不同的任务，因此多个任务可以重叠。时间并行通常被称为流水线(pipelining)。空间并行有时也被称为并行(parallelism)，但是我们会避免这种叫法，因为有二义性。

考虑一个具有延迟$L$的任务。在没有并行性的系统中，吞吐量为$1/L$。在一个具有$N$个硬件副本的空间并行系统中，吞吐量为$N/L$。在一个时间上并行的系统中，任务被理想地分成了$N$个相等长度的步骤或阶段。在这种情况下，吞吐量同样为$N/L$，并且只需要一份硬件副本。然而，找到$N$个相等长度的步骤通常是不切实际的。如果最长的步骤具有延迟$L1$，则流水线式的吞吐量为$1/L_1$。

流水线处理(时间上的并行性)特别吸引人，因为它加速了电路而无需复制硬件。相反，寄存器被放置在组合逻辑块之间，将逻辑划分为较短的阶段，这些阶段可以以更快的时钟运行。这些寄存器防止了一个流水线阶段中的令牌赶上并损坏下一个阶段中的令牌。

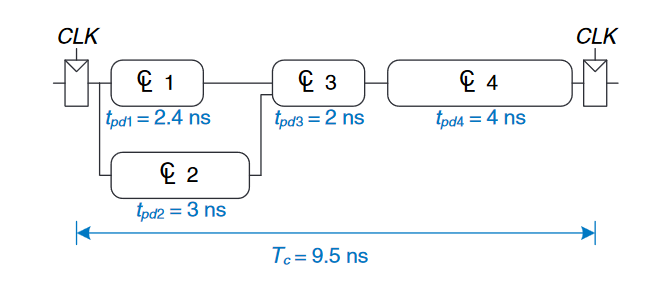
下图展示了没有流水线处理的电路的例子。其在寄存器之间包含了四个逻辑块，关键路径通过了$2, 3, 4$。假设这个寄存器的时钟沿到$Q$的传播时延为$0.3ns$和设置时间是$0.2ns$，那么其周期时间为$T_c = t_{pcq} + t_{pd} + t_{setup} = 0.3 + 3 + 2 + 4 + 0.2 = 9.5ns$。因此，该电路的延迟为$9.5ns$，吞吐量为$1/9.5ns = 105MHz$。

no pipelining

下图的第一张图展示了一样的电路，不过有一个二级流水线，通过在第三和第四组合电路之间添加寄存器。第一部分的最小时钟周期为$T_{c1} = 0.3 + 3 + 2 + 0.2 = 5.5ns$，第二部分的最小时钟周期为$T_{c2} = 0.3 + 4 + 0.2 = 4.5$。时钟必须足够慢，使得所有阶段都能工作，因此$T_c = max{T_{c1}, T_{c2}} = 5.5ns$。其延迟为两部分之和，即$11ns$，吞吐量为$1/5.5ns = 182MHz$。这个例子表明，在一个真实的电路中，具有两个阶段的流水线几乎使吞吐量翻倍，并略微增加了延迟。相比之下，理想的流水线处理会在不增加延迟的情况下确实使吞吐量翻倍。这种差异是因为电路无法被精确地划分为两个完全相等的部分，以及因为寄存器引入了更多的顺序开销。

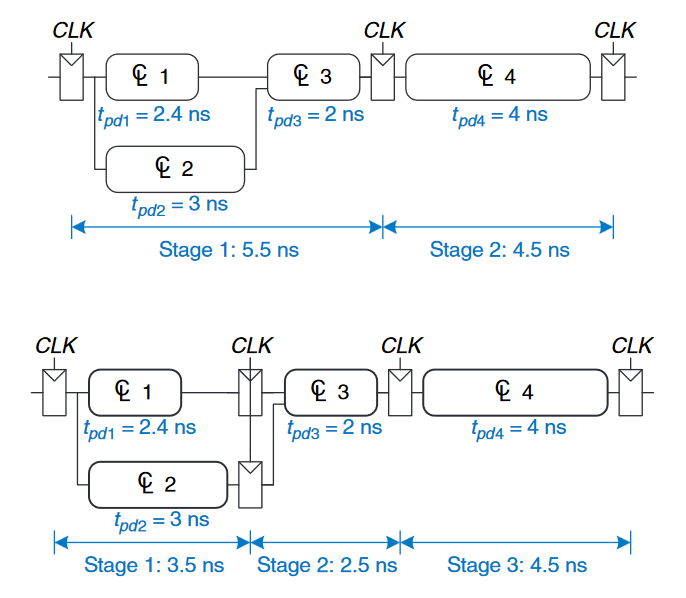
has pipelining

上图的第二张图显示了一个三级流水线，值得注意的是，在第一个流水线阶段结束时，需要两个寄存器来存储块$1$和块$2$的结果。可以看出，周期时间被第三阶段限制为$T_c = T_{c3} = 4.5ns$，延迟为$11.5ns$，吞吐量为$1/4.5=222MHz$。因此，增加一个流水线阶段以牺牲部分延迟的代价来提高吞吐量。

尽管这些技术非常强大，但并不适用于所有情况。并行性的祸根是依赖关系。如果当前任务依赖于先前任务的结果，而不仅仅是当前任务中的先前步骤，那么任务在先前任务完成之前就无法启动。例如，如果本想要在开始准备第二批饼干之前先检查第一批饼干的味道是否好，那么他就有了一个依赖关系，这将阻止流水线处理或并行操作。并行性是设计高性能数字系统的最重要技术之一。