Raft: An Understandable Consensus Algorithm

Raft是一个用于管理$replicated log$的算法，其通过$electing a leader$，并赋予该$leader$管理$replicated log$的完全权限来实现一致性。该$leader$会从客户端接收$log entries$，并将其复制到其他服务器上同时告知服务器该$log entries$何时能够安全地被它们的$state machine$所使用。

Raft通过$electing a leader$这样的方式来简化管理$replicated log$。$leader$可以在不咨询其他服务器的情况下决定日志中放置$new log entry$的位置，并且数据以一种简单的方式从$leader$流向其他服务器。
一个$leader$可以失败或者与其他服务器断开连接，在这种情况下，一个新的$leader$将会被$electing$。

通过$leader$这样的方式，$Raft$将一致性问题分解为了三个相对独立的子问题：

• $Leader Election$
  • 当一个现存的$leader$失败时，一个新的$leader$必须被$electing$
• $Log Replicated$
  • $leader$必须能够从客户端中接收$log entries$，并且将其复制到集群中，同时强制其他集群日志与$leader$保持一致
• $Safety$
  • $Raft$的关键$safety property$是下图所给出的状态机的$safety property$：如果任何服务器将特定的$log entry$应用到其状态机，那么其他服务器都不能对相同的日志索引应用不同的命令。

Raft Basics

一个$Raft$集群包含了数个服务器，通常而言，我们用五个服务器作为一个集群，这就使得该集群系统能够容忍两次错误。

这是因为 Raft 使用多数投票原则来决定集群的$leader$和状态更新。在 5 台服务器的集群中，即使 2 台服务器失效，剩下的 3 台服务器依然能够形成多数（3 台服务器中的多数为2），继续提供服务。这使得系统具有一定的容错能力，即可以在部分服务器故障的情况下，保证数据一致性和可用性。

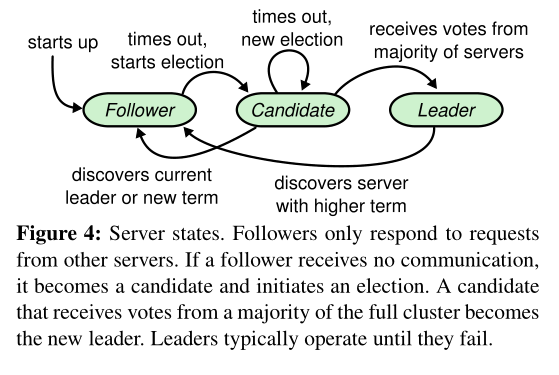
在任给的时间内，每一个服务器都只能有三个状态中的其中一个状态：$leader$，$follower$或者$candidate$。在一个正常的操作中，系统中恰好只有一个$leader$，而其他服务器都是$follower$。$follower$是被动的，因此他们不会主动发出任何请求，只是响应来自$leader$和$candidate$的请求。$leader$处理所有客户端的请求(如果客户端与$follower$相连，$follower$会将其重定向到$leader$)。第三种状态是$candidate$，用于选举出新的$leader$，这将会在下一个小结描述，现在给出其状态和转换图例：

$Raft$将时间划分为任意长度的$Terms$，如下图所示。$Terms$被一个连续的整数所编号。每一个$Terms$都以一个$election$开始，该$election$中，一个或多个$candidate$尝试成为$leader$。如果一个$candidate$在$election$中胜出，那么他会在$Term$的剩余时间内胜任$leader$。

在某些情况下，$election$会导致投票(vote)出现分歧。一旦处于这种情况，该$Term$内将以$no leader$的情况结束；新的$Term$(带有新的$election$)将会很快开始。$Raft$确保在给定$Term$内最多只有一个$leader$。

$election$可能出现投票分裂：这就意味着多个$candidate$得到了相同数量的选票
$Raft$确保在每个$Term$内，最多只有一个$leader$

不同服务器之间可能在不同时间观察到$Term$之间的转换，在某些情况下，某个服务器可能无法观察到某次$election$，甚至错过整个$Term$。$Term$在$Raft$中充当一个$logic\ clock$，这使得服务器能够检测过时的信息，例如失效的$leader$。每个服务器都会存储一个$current\ term\ number$，并且这个$number$随着时间单调递增。

在这里，$logic\ clock$指的是一种用于排序事件发生顺序的机制。在 $Raft$ 中，$Term\ number$充当$logic\ clock$，帮助服务器跟踪系统状态并识别过时信息。通过增加的$Term\ number$，服务器能够判断哪些信息是最新的，从而避免与过时的领导者或数据进行交互。这种机制确保系统的一致性和稳定性，尽管服务器之间的观察顺序可能不同

$current\ term\ number$在服务器通信时会被交换；如果一个服务器的$current\ term\ number$比另一个服务器的小，他会将自己的$term\ number$更新为较大的值。如果一个$candidate$或$leader$发现自己的$Term$过期，则其会立即退回到$follower\ state$。如果一个服务器收到了带有过期的$term\ number$的请求，则会拒绝该请求。

$Raft$服务器之间通过$RPCs$协议进行通信，对于最为基础的$Raft$一致性算法只要求了两种类型的$RPCs$。

• $RequestVote\ RPCs$由$candidate$在$election$期间发起
• $AppendEntries\ RPCs$由$leader$发起的，用于复制$log\ entries$，并提供一种$heartbeat$机制。

$heartbeat$机制是分布式系统中的一种通信方式，用于维护节点之间的活跃状态和协调。

如果服务器没有及时收到响应，它们会重试$RPCs$，并且会并行地发出$RPCs$以获得最佳性能。

Leader election

$Raft$使用$heartbeat$机制来触发$election$。当服务器启动时，他们会作为$follower$开始运行。只要服务器从leader或candidate收到有效的$RPCs$，他就会保持在$follower\ state$。$leader$会定期向所有跟随者发送$heartbeat$(也就是不包含$log\ entries$的$AppendEntries\ RPCs$)以维持其领导权。如果一个$follower$在一段时间内没有收到任何通信，他将假设当前没有有效的$leader$，并开始一次$election$以选出新的$leader$

这里就给出了$heartbeat$机制的细节：

保持$leader\ state$：$leader$定期向$follower$发送$heartbeat$(即不带$log\ entry$的$AppendEntries\ RPCs$），以表明自己仍然是有效的$leader$。
检测失效：如果$follower$在一定时间内没有收到来自$leader$的$heartbeat$，它们可能会认为$leader$已经失效，并触发新的$election$。
更新$Term$：$heartbeat$中包含$current\ term\ number$，这有助于$follower$更新其状态，确保它们不会与过时的$leader$进行交互。
维护一致性：通过定期的$heartbeat$，系统能够及时检测并处理节点之间的状态变化，维护系统的一致性和可用性

开始$election$时，$follower$会增加他自身的$current\ term\ number$并且转变为$candidate\ state$。然后会为自己投票，并且并行地发送$RequestVote\ RPCs$给集群中的每一个服务器。$candidate$状态会一直持续，直到发生以下事件中的其一：

• 他在$election$中胜出
• 另一个服务器胜出并成为$leader$
• 在一段时间内没有任何胜出者

如果一个$candidate$在相同的$Term$内收到了在整个集群中的大部分服务器的$vote$，那么就认为该$candidate\ wins\ an\ election$。每一个服务器至多可以投票给一个$candidate$，根据先来后到原则。$majority\ rule$确保了在一个特定$Term$内，至多只有一个$candidate$在这次$election$中获胜。一旦一个$candidate$赢得这次$election$，他就会立即变为$leader$，并且发送$heartbeat$信息给其他所有服务器以建立其权力和阻止新的$election$。

在等待投票期间，$candidate$可能会收到来自另一个服务器的$AppendEntries\ RPCs$，该服务器声称自己是$leader$。如果该$leader$的$Term$(包含在$AppendEntries\ RPCs$中)至少与$candidate$的$current\ term\ number$一样大，那么$candidate$就会认可该$leader$的合法性并回到$follower$状态。如果小于$candiate$的$current\ term\ number$，则$candidate$会拒绝该$RPCs$并继续保持在$candidate$状态。

第三种可能的结果是$candidate$既没有赢得也没有输掉$election$：如果有许多$follower$同时成为$candidate$，选票可能会分散，导致没有$candidate$获得多数票。当这种情况发生时，每个$candidate$都会超时，并通过增加其$Term$并发起新一轮的 $RequestVote\ RPCs$ 来开始新一轮$election$。然而，如果没有额外的措施，选票分裂的情况可能会无限期地重复下去。

$Raft$使用$randomized\ election\ timeouts$(随机选举超时)来确保投票分裂很少发生并且其会在短时间内结束。为了防止选票分裂，$election$超时时间试从一个固定区间中随机选取的($eg. 150 ~ 300ms$)。这使得服务器的超时时间分散开来，从而在大多数情况下只有一个服务器会超时；它赢得$election$并在其他服务器超时之前发送$heartbeat$。相同的机制也用于处理选票分裂。每个候选人在$election$开始时都会重新启动其随机化的选举超时时间，并等待该超时结束后再开始下一次$election$；这减少了在新一轮$election$中再次发生选票分裂的可能性。

Log Replication

一旦一个$leader$被选择出来，他就会开始处理客户端请求。每一个客户端请求都包含一个会由$RSM$($replicated\ state\ machine$)执行的命令。$leader$会追加这些命令作为一个新的$entry$到自身的$log$中，然后并行地调用$AppendEntries\ RPCs$以复制该$entry$到其他服务器上。当$entry$被安全复制后，$leader$将该$entry$应用到其状态机，并将执行结果返回给客户端。如果$follower$崩溃、运行缓慢或网络数据包丢失，$leader$会无限期地重试$AppendEntries\ RPCs$，直到所有$followers$最终存储了所有的$log\ entries$。

$log$的组织方式如下图所示，每个$log\ entry$存储一个状态机命令以及该条目被$leader$接收时的$term\ number$。$log\ entry$中的$term\ number$用于检测$log$之间的不一致性，并确保一些特性得到保障。每一个$log\ entry$也会有一个整数索引来标识在$log$中的当前位置信息。

$leader$决定何时将$log\ entry$安全地应用到状态集中，这样已经被应用的$log\ entry$被称为$committed$。$Raft$保证$committed$是持久的，并且最终会在所有可用的状态机上执行。当创建该$log\ entry$的$leader$将其复制到大多数服务器上时，该$log\ entry$就被认为是$committed$（如上图所示的$entry\ 7$）。这也会提交$leader’s\ log$中所有先前的$entries$，包括由之前的$leader$创建的$entries$。下一节会讨论在$leader$变更后应用此规则的一些细微之处，并且表明这种$commit$的定义是安全的。$leader$跟踪其已知的$committed$的$highest\ index$(最高索引)，并在未来的$AppendEntries\ RPCs$(包含$heartbeat$)中包含该索引，以便其他服务器最终得知。一旦$follower$得知$log\ entry$已被$committed$，他将按日志顺序将该条目应用到本地状态机中。

这种机制不仅简化了系统的行为，并且使其更容易预测，而且是确保安全性的重要组件。Raft维护了以下属性，这些属性共同构成了$Log\ Matching\ Property$：

• 如果在不同$log$的两条$entry$具有相同的$index$和$term$，那么它们存储相同的$command$
• 如果在不同$log$的两条$entry$具有相同的$index$和$term$，那么它们所有前面的$entries$都是相同的

第一个属性源于$leader$在给定任期内至多只能创建一个具有特定$log\ index$的$entry$，并且$log\ entries$在$log$中的位置永远不会发生变化。第二个属性通过$AppendEntries\ RPCs$执行的简单一致性检查得以保障。在发送$AppendEntries\ RPCs$时，$leader$包括其$log$中紧接着新$entry$之前的$entry$的$index$和$Term$。如果$follower$在其$log$中未找到具有相同$index$和$Term$的$entry$，则会拒绝新的$entry$。这个一致性检查充当了归纳步骤：$log$的初始空状态满足$Log\ Matching\ Property$，并且一致性检查在扩展$log$时保留$Log\ Matching\ Property$。因此，每当$AppendEntries\ RPCs$返回成功时，$leader$就知道$follower$的$log$与他自己的$log$在新的$entry$之前时相同的。

在正常运行期间，$leader$和$follower$的日志保持一致性，所以$AppendEntries\ RPCs$的一致性检查不会失败。然而，$leader$故障会使得$log$不一致(之前的$leader$可能没有完全复制其$log$中的全部$entries$)。这些不一致性可以在一些列的$leader$和$follower$故障中累积。这张图片说明了$follower$与新的$leader$上的$log$的差异。$follower$可能缺少$leader$中存在的$entries$，或者可能拥有$leader$所不存在的额外的$entries$，或者两者都有。$log$中的缺失和额外$entry$可能跨越多个$Term$。

在$Raft$中，$leader$通过强制$follower’s\ log$复制自身的$log$来处理不一致性。这就意味着在$follower$中发生冲突的$entry$会被来自于$leader$中的$entry$所覆盖。在下一个小节中会讲述增加一些限制会使得其确保是安全的。

为了使$follower’s\ log$与自己的$log$保持一致，$leader$必须找到两个日志一致的最新的$log\ entry$，删除$follower$的$log$中该节点之后的任何$entries$，并将该点之后的所有$leader$的$entries$发送给$follower$。

这里需要意识到，如果$follower$中在相同$term$和$index$下有$commit$与$leader$中的不一致，这就违反了$Log Matching Property$属性，就说明$follower$在这之后是有问题的，因此删掉该点之后的所有$entry$，复制下$leader$的后续$entry$以确保一致性

所有这些操作都是响应$AppendEntries\ RPCs$执行的一致性检查。$leader$为每个$follower$维护一个$nextIndex$，它是$leader$将发送给该$follower$的下一条$log\ entry$的$index$。当$leader$首次上任时，他将所有$nextIndex$的值初始化为其$log$中的最后一个$entry$的$index$之后的$index$(如下图中的11)。如果$follower$的$log$与$leader$的不一致，那么在下一个$AppendEntries\ RPCs$中，一致性检查将会失败。在拒绝接收之后，$leader$会将$nextIndex$减少并重传$AppendEntries\ RPCs$。最终$nextIndex$将到达一个点，在该点上$leader$和$follower$的$log$匹配。当这种情况发生时，$AppendEntries\ RPCs$将成功，这将删除$follower’s\ log$中的任何冲突$entries$，并将$leader’s\ log$中的$entries$追加到$follower$中(如果有的话)。一旦$AppendEntries\ RPCs$成功，$follower’s\ log$将会与$leader$的一致，并在剩余的$Term$内保持一致。

如果有需要，可以优化协议来减少被拒绝的$AppendEntries\ RPCs$数量。

有了这种机制，$leader$上任时不需要采取任何特殊行为来恢复$log$的一致性。他只需要开始正常操作，$log$会自动根据$AppendEntries\ RPCs$一致性检查的失败而趋于一致。$leader$永远不会覆盖或删除自己的$log’s entries$(比如这张图中的$Leader\ Append-Only\ Property$)

Safety

上一个小节中描述了$Raft$如何选举出$leader$和复制$log\ entries$。然而，以目前描述的机制还不足以确保让每一个状态机在同一个顺序中运行相同的命令。例如，一个 $follower$ 可能在 $leader$ 提交多个$log\ entries$ 时不可用，然后它可能被选为 $leader$，并用新的 $entries$ 覆盖这些旧的$entries$；结果，可能会导致不同的状态机执行不同的命令序列。

这个小节就会通过增加一个限制来完善$Raft$算法，该限制能够表明哪些服务器可以被选为$leader$。这个限制确保了在任何给定$Term$内的$leader$包含所有在上一个$Term$中的$commit$(如这张图中的$Leader\ Completeness\ Property$)。

Election Restriction

在任何$leader-base$的共识算法中，$leader$最终必须存储所有已提交的$log\ entries$。$Raft$采用了一种更为简单的方式，它确保每一个新$leader$从选举时起就包含上一个$Term$的所有已提交的$entries$，而无需将这些$entries$传输给$leader$。这意味着$log\ entries$只朝一个方向流动($leaders \rightarrow follower$)，并且$leaders$永远不会覆盖$log$中现有的$entries$。

$Raft$试用投票过程来防止$candidate$赢得选举，除非他的$log$包含所有的$committed$。$candidate$必须联系集群中的大多数节点才能被$elected$，这就意味着每个$committed$必须至少存在于其中一个服务器上。如果$candidate$的$log$至少与多数中的任何其他$log$一样$up-to-date$(这将在稍后介绍)，那么该$candidate$将包含所有的$committed\ entries$。$RequestVote RPCs$实现了这一限制：该$RPCs$包含了关于$candidate’s\ log$的信息，如果投票者自己的$log$比$candidate$的更新，则拒绝投票。

$Raft$通过比较$log$中最后$entry$的$index$和$Term$来确定两个$log$哪一个更$up-to-date$。
如果$log$的最后的$entry$具有不同的$Term$，则$Term$较大(较晚)的$log$为$up-to-date$。
如果$log$的最后的$entry$具有相同的$Term$，则$index$较大的(较长)$log$为$up-to-date$。

Committing entries from previous terms

就如之前所描述的一样，$leader$知道一旦在大多数服务器上都存储了来自$current\ term$的$entry$，那么这条$entry$就是$committed$的。如果$leader$在提交$entry$之前就崩溃了，那么下一个$leader$就会尝试完成对这条$entry$的复制。然而，现在的$leader$不能立即认为：一旦来自上一个$Term$的$entry$在大多数服务器上存储，那么该$entry$就是$committed$的。下图就解释了这一种情况，其中一个旧的$log\ entry$存储在大多数服务器上，但仍然可能被下一个$leader$覆盖。

上图中展示了这样一个问题：如果$S1$在(c)情况发生了崩溃，尽管此时$[2]$已经被复制到大多数服务器上，但其仍不是$committed$的；(在(d)这种情况，$S5$被选为$leader$，此时$S5$会复制$[3]$给其他服务器，导致$[2]$丢失；如果$S1$在(e)这种情况下，$S1$在崩溃前在$Term3$时复制了一条$entry$，并且该$entry$被$committed$，即使$S1$崩溃，那么这时$S5$就不再会被选为$leader$)。

为了消除像上图中的问题，$Raft$不通过计数复制的$entry$来提交来自上一个$Term$的$log\ entry$。只有来自$leader$的$current\ term\ number$的$log\ entry$才能够通过计数复制的$entry$被$committed$；一旦以这种方式提交了$current\ term$的$entry$，所有之前的$entry$就会因为$Log Matching Property$而间接提交($Log Matching Property$要求了如果在不同$log$的两条$entry$具有相同的$index$和$term$，那么它们所有前面的$entries$都是相同的)。在某些情况下，$leader$就可以安全地得出结论：认为一个旧的$log\ entry$是$committed$的，但$Raft$采取了更为保守的方法以简化实现。

$Raft$在提交规则中增加了这一额外的复杂性，因为$log\ entry$在$leader$复制来自上一个$Term$的$entry$时保留了其原始的$Term\ number$。在其他共识算法中，如果新的$leader$重新复制来自上一个$Term$的$entry$，则必须使用其新的$Term\ number$。此外，$Raft$中的新的$leader$发送的来自上一个$Term$的$log\ entry$比其他算法少。

Safety Argument

鉴于$Raft$算法的完善，我们现在可以更精确地论证$Leader\ Completeness\ Property$的成立。我们先假设该属性没有成立，然后我们逐步证明这是矛盾的。假设一个$Term\ T$的$leader$(记作$leader_T$)在他的$Term$内提交了$log\ entry$，但是该$log\ entry$没有被之后某个$Term$的$leader$所存储。考虑最小的$Term\ U \gt T$，其中$leader_U$没有存储该$log\ entry$。

$Leader\ Completeness\ Property$
如果在给定$Term$中提交了一条$log\ entry$，那么该$entry$将会出现在所有$higher-number\ Term$的$leader$的$log$中

1. $leader_T$提交的$entry$在$leader_U$当选时必须缺失($leader$不会删除或覆盖$entry$)
2. $leader_T$在集群的多数节点上复制了该$entry$，而$leader_U$也从集群的多数节点获得了投票。因此，至少有一个服务器既接收了来自$leader_T$的$entry$，又投票给了$leader_U$，如上图所示。该投票者是出现矛盾的关键
3. 该投票者在投票给$leader_U$之前必须接受来自于$leader_T$的$committed\ entry$；否则他会拒绝来自$leader_T$的$AppendEntries\ RPCs$请求(因为他的$current\ term$比$leader_T$更高)
4. 该投票者在投票给$leader_U$时仍然存储该$entry$，因为假设每个中间$leader$都包含了该$entry$，需要注意$leader$永远不会删除$entry$，而$follower$仅在$entry$与$leader$冲突时才会被删除
5. 该投票者投票给$Leader_U$的前提之一是：$leader_U$的$log$必须与投票者的一样最新，这样就导致了一个矛盾。
6. 首先，如果该投票者和$leader_U$共享相同的$last\ log\ term$，则$leader_U$的$log$必须至少与投票者的$log$一样长，因此其$log$包含了投票者$log$中的每一条$entry$。这是矛盾的，因为我们假设投票者包含了$committed\ entry$，而$leader_U$不包含。
7. 否则，$leader_U$的$last\ log\ term$必须大于投票者的。此外，它还必须大于$T$，因为投票者的$last\ log\ term$至少为$T$(因为其包含了来自于$term\ T$的$committed\ entry$)。根据假设，创建$leader_U$的$last\ log\ entry$的之前的$leader$必须在其$log$中包含$committed\ entry$。然后根据$Log\ Matching\ Property$，$leader_U$的$log$也必须包含该$committed\ entry$，者又是一个矛盾。
8. 因此，所有大于$Term\ T$的$leader$必须包含所有在$Term\ T$内的$committed\ entry$
9. 而$Log\ Matching\ Property$确保未来的$leader$也将包含间接的$committed\ entry$

Follower and Candidate crashes

到目前为止，我们专注于$leader$发生了故障的问题。$follower$和$candidate$的崩溃比$leader$的崩溃要简单得多，而且两者的处理方式相同。如果$follower$或$candidate$崩溃，那么将发送给他的$RequestVote$和$AppendEntries RPCs$失败。$Raft$通过无限重试来处理这些故障；如果崩溃的服务器重新启动，那么$RPCs$将成功完成。如果一个服务器在完成$RPCs$后但在响应之前崩溃，那么他在重启之后会再次收到相同的$RPC$。$Raft\ RPCs$是幂等($idempotent$)的，因此这不会造成任何损害。例如：如果一个$follower$收到一个包含已在其$log$中的$log\ entry$的$AppendEntries\ RPCs$请求，它会忽略掉新请求中的$entries$。

Idempotent
幂等是指在多次执行相同操作时，结果保持不变的特性。在网络请求中，如果一个请求是幂等的，无论它被执行多少次，最终状态都是一致的，不会造成额外的影响。这样可以确保系统在出现故障时的可靠性。

Timing and Availability

对于$Raft$而言，其中一个要求便是其安全性不能依赖于时序：系统不能因为某些事情发生得比预期快或慢而产生不正确的结果。然而，可用性($availability$，系统及时响应客户端的能力)不可避免地依赖于时序。例如，如果消息交换所需的时间超过服务器崩溃之间的典型时间，$candidate$将无法持续足够长的时间以赢得$election$；没有稳定的$leader$，$Raft$将无法继续。

$leader election$是$Raft$中时序最为关键的方面。只要系统满足以下时序要求，$Raft$就能$election$并维持一个稳定的$leader$:

$$
broadcastTime \ll electionTimeout \ll MTBF
$$

在上面的不等式中，$broadcastTime$是服务器并行向集群中的每个服务器发送$RPCs$并接收响应的平均时间；$electionTimeout$是在Leader Election小节中所描述的$election$超时；$MTBF$是单个服务器的平均故障间隔时间。$broadcastTime$应比$electionTimeout$小几个数量级，以便$leader$可以可靠地发送$heartbeat$，从而防止$follower$启动$election$；考虑到随机化的选举超时方法，这个不等式也使得分裂投票变得不太可能。$electionTimeout$应比 $MTBF$ 小几个数量级，以确保系统能够持续稳步推进。当$leader$崩溃时，系统将在大约$electionTimeout$内不可用；我们希望这仅占总时间的一小部分。

$broadcastTime$和 $MTBF$ 是底层系统的属性，而 $electionTimeout$ 是我们必须选择的参数。$Raft$ 的 $RPCs$ 通常要求接收方将信息持久化到稳定存储中，因此广播时间可能在 $0.5 ~ 20ms$之间，具体取决于存储技术。因此，$electionTimeout$ 可能在 $10 ~ 500ms$之间。典型的服务器 $MTBF$ 通常为几个月或更长，这很容易满足时序要求。

Appendix A

• 选举过程
  • 假设一开始都是$follower$状态，其都有一个$electionTimeout$，当任一$follower$到达$electionTimeout$时，其会立即转变为$candidate$状态，